3.1 Introduction and Synopsis

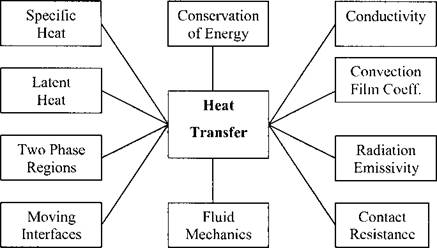
The conservation of energy is the fundamental principle in thermal analysis. Therefore in heat transfer theory, we are concerned with energy and ignore stress, strain and displacement. The principal phenomena are shown in Figure 3-1.

The temperature field in the neighborhood of weld pool can be obtained by specifying the heat input. We will see that all weld heat source models based solely on the heat equation, specify either the source term Q, or choose a boundary of the domain near the weld pool and prescribe the temperature or prescribe the flux q on that boundary. Each of these must be specified as functions of time and position. While one can choose various types of functions, e. g., Gaussian, polynomials, Fourier series, Legendre polynomials, spherical harmonics, etc., to represent the function, which type of function is chosen is in a sense secondary. It is secondary in the sense that any function can be expressed as a linear combination of functions in any complete function space. For example, any reasonable function can be expressed in terms of a Fourier series. In a sense this is similar to the point that any problem that can be posed and solved in a Cartesian coordinate system, can also be solved in other coordinates systems such as cylindrical, spherical, ellipsoidal, toroidal, etc. Some choices may be more convenient and the equations may look simpler and could be easier to solve. However, the fact remains that if the problem can be solved in one coordinate system, it can be solved in any other equivalent coordinate system.

When we discuss a model for a heat source, it is worth distinguishing what is intrinsic to the model, i. e., what is true for all coordinate systems, and what depends on the representation and on the choice of a particular coordinate system. This is not to argue that the choice of coordinate system, e. g., Cartesian or cylindrical, and the choice of function space, e. g., Fourier series or Gaussian functions, does not matter. It is to argue that the time to make this choice is after choosing the intrinsic model.

If there are no phase changes and the thermal conductivity and specific heat are strictly positive, then given initial conditions, boundary conditions and a domain with a reasonably smooth boundary, one can show mathematically that the solution of the heat equation exists and is unique. If there are phase changes, such as dendrite formation during solidification, then the solution exists but need not be unique. One reason for this lack of uniqueness is that we cannot know, at least not yet, the distribution of nuclei. Another is that dendrite branching might not be unique.

Ignoring for the moment the question of how accurately the problem can be solved, let us note that there are only a small number of parameters involved in the heat equation. Therefore the number of types of intrinsic heat source models that could be developed is very small.

In any real weld, one can argue from physics that a real temperature field does exist. If one had sufficiently accurate sensors, this real temperature field could be measured accurately. If this temperature field is sufficiently smooth, say continuous with a piecewise continuous spatial temperature gradient, then the energy equation can be written in a variational form. This is the form usually used in finite element analysis (FEM). If second derivatives are piecewise continuous, then the energy equation can be written in the form of a partial differential equation (PDE). Finite difference methods (FDM) are usually based on the PDE form. Normally, a thermal problem is posed by specifying the domain, material parameters such as thermal conductivity, specific heat, latent heats, initial conditions and boundary conditions. Then the solution of this problem is the temperature and phase fractions at all points (x, y,z, t) in the space-time domain. Here we have used the notation of a Cartesian coordinate system for space and time but any coordinate system will serve equally well. If we ignore phenomena such as dendrite formation, then it is well known that this solution is unique.

If the reader has accepted our assumptions that in a region of space that we call a domain, the solution exists and is unique, then the problem can be posed in several equivalent forms. Note that here our assumption of existence and uniqueness is based on physics not mathematics. In particular, if we know the solution, i. e., temperature as a function of (x, y,z, t), then we can evaluate the energy equation directly to determine, initial conditions for any time, boundary conditions for any choice of a sub-domain of the full domain, and distributed heat input for any region. The most obvious choices are that the boundary conditions can be stated either in terms of fluxes, i. e., Neumann Boundary Conditions (BCs), or in terms of prescribed temperatures, i. e., Dirichlet BCs. If the distributed heat input is not zero and is in the domain, then the value given by the heat equation must be used as is. There is no alternative. A very important point is that the thermal problem can be solved on any sub-domain of the full domain. We emphasize that for all of these choices, only one solution exists. Here there is no notion of approximation or error analysis involved. Here we consider only exact solutions. At this point, the various choices appear to have equal value.