Theoretical Formulations

The basic theory of heat flow that was developed by Fourier and applied to moving heat sources by Rosenthal [38] and Rykalin [37] in the late 1930s is still the most popular analytical method for calculating the thermal history of welds. As many researchers have shown, Rosenthal’s point or line heat source models are subject to a serious error for temperatures in or near the fusion zone (FZ) and heat affected zone (HAZ). The infinite temperature at the heat source assumed in this model and the temperature sensitivity of the material thermal properties increases the error as the heat source is approached. The effect of these assumptions and others on the accuracy of temperature distributions from the Rosenthal analysis has been discussed in detail by Myers et al. [39].

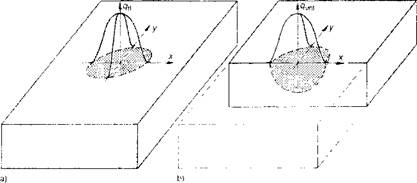
To overcome most of these limitations several authors have used the finite element method (FEM) to analyze heat flow in welds. Since Rosenthal’s point or line models assume that the flux and temperature is infinite at the source, the temperature distribution has many similarities to the stress distribution around the crack tip in linear elastic fracture mechanics. Therefore many of the FEM techniques developed for fracture mechanics can be adapted to the Rosenthal model. Certainly it would be possible to use singular FEM elements to analyze Rosenthal’s formulation for arbitrary geometries. This would retain most of the limitations of Rosenthal’s analysis but would permit complex geometries to be analyzed easily. However, since it would not account for the actual distribution of the heat in the arc and hence would not accurately predict temperatures near the arc, this approach is not pursued here. Pavelic et al. [40] first suggested that the heat source should be distributed and he proposed a Gaussian distribution of flux deposited on the surface of the workpiece. Figure 2-5 represents a circle surface heat source and a hemispherical volume source, both with Gaussian normal distribution (bell shape curves), in a mid-thick plate. The geometrical parameters of heat flux distribution are estimated from the results of weld experiments (molten zone, size and shape and also temperature cycle close to molten zone).

The subsequent works of Andersson [41], Krutz and Segerlind [42] and Friedman [43] are particularly notable. In References [42] and [43] Pavelic’s ‘disc’ model is combined with FEM analysis to achieve significantly better temperature distributions in the fusion and heat affected zones than those computed with the Rosenthal model.

While Pavelic’s ‘disc’ model is certainly a significant step forward, some authors have suggested that the heat should be distributed throughout the molten zone to reflect more accurately the digging action of the arc. This approach was followed by Paley [44] and Westby [45] who used a constant power density distribution in the fusion zone (FZ) with a finite difference analysis, but no criteria for estimating the length of the molten pool was offered. In addition, it is difficult to accommodate the complex geometry of real weld pools with the finite difference method.

The analyst requires a heat source model that accurately predicts the temperature field in the weldment. A non-axisymmetric three­dimensional heat source model which is proposed in this book achieves

this goal. It is argued on the basis of molten zone observations that this is a more realistic model and more flexible than any other model yet proposed for weld heat sources. Both shallow and deep penetration welds can be accommodated as well as asymmetrical situations.

The proposed three-dimensional ‘double ellipsoid’ configuration heat source model is the most popular form of this class of heat source models [46]. It is shown that the ‘disc’ of Pavelic et al [40] and the volume source of Paley and Hibbert [44] and Westby [45] are special cases of this model. In order to present and justify the double ellipsoid model, a brief description of the Pavelic ‘disc’ and of the Friedman [43] modification for FEM analysis is necessary. In addition, the mathematics of the disc is extended to spherical, ellipsoidal and finally to the double ellipsoidal configuration. Finally, it is pointed out the most general form of this class of model has a general heat source distribution function.