СМЕШЕНИЕ В ЗОНЕ ДОЗИРОВАНИЯ (ВЫДАВЛИВАНИЯ)
 19 ноября, 2013
19 ноября, 2013  admin
admin Окончательное смешение расплавов полимеров с добавками (ингредиентами) происходит в зоне дозирования одношнекового •кструдера. При этом за начальную толщину полос г0 в этой зоне « в дует принимать толщину полос в конце зоны плавления. Отличи гельной особенностью поведения расплава в этой зоне является и* что в винтовом канале частицы полимера принимают участие в циркуляционном течении не только в поперечном сечении кана-
i. i по и вдоль канала (винтовой механизм движения расплава). При этом вклад в процесс смешения циркуляционного характера
движения расплава весьма существенен |И, 46|. При рассмотрении процесса смешения в зоне плавления (переходной зоне) влиянием циркуляции на процесс можно пренебречь, так как интенсивная циркуляция имеет место только в конце указанной зоны 113, 20. 22, 23, 25, 32, 49, 55). Согласно теории ламинарного смешения 147) качество смеси однозначно определяется величиной деформации сдвига, развивающейся в расплаве полимера в процессе его течения по винтовому каналу шнека. В работах |6, 7, 10, II, 48, 55) развиты различные подходы к определению величины деформации сдвига.
Г. Шенкель |48) определяет качество смеси в одноишековых экструдерах по наименьшему сдвигу, получаемому бесконечно малым элементом жидкости в винтовом канале шнека. В качестве такого бесконечно малого элемента Г. Шенкель выбрал частицу с координатой у = (2/3)/? (см. раздел 2.7), поперечная составляющая
vJ 2. =0 . Эта части - j
на жидкости не участвует в циркуляции и имеет минимальное время пребывания в винтовом канале. Остальные частицы участвуют как в поперечных, так и в продольных циркуляциях жидкости, и время их пребывания в канале шнека больше времени пребывания в канале частицы с координатой у = (2/3)/;. Следовательно, указанные частицы подвергаются минимальному сдвигу и будут хуже перемешаны с остальными.
Метод Г. Шенкеля предполагает, что в остальном объеме жидкости качество смеси лучше, так как он подвергается большему сдвигу. Указанный метод применим в инженерных расчетах только в том случае, если качество смеси, определенное в точке с координатой у = (2/3)Л, удовлетворяет предъявляемому к смеси требованию по однородности состава. Он также может быть применен при теоретическом анализе процесса смешения в зоне плавления, где влиянием циркуляции можно пренебречь.
Таким образом, при расчете перемешивающей способности одношнекового экструдера по методу Г. Шенкеля необходимо рассчитать величину сдвига, получаемого частицей жидкости с координатой у - (2/3)/;. Величина этого сдвига равна:
|
где а = y/h. |
скорости потока которой равна нулю
|
/ |
2 |
/ |
2 |
|
|
3v.| |
+ |
dvx |
•/ |
|
|
гч 1 II & |
ду |
2 а=— |
||
|
^ 3J |
3J |
|
и Ы I дУ аЛ * |
|
можно иолу- |
|
3 3 |
|
Значения градиентов скорости ду |
|
dvz |
чип, дифференцированием уравнений для vz и vy по. v с учетом иы ражен ий для vc. и v^.
13 уравнении (2.263) ’(]Л — это время пребывания контрольной частички в зоне дозирования; оно равно:
'I 2=-i——-
'а~ч vA 2-sina 3
I m - /. - длина зоны дозирования шнека вдоль его оси.
Тогда
I 4sin2a + (l + fl2 )cos2a
Г = ,*5Т—71-------------- Г ----- • <2-264)
/ту (l-o)smacosa
Г Шенкель считает, что величина сдвига бесконечно малого помента расплава полимера с координатой а = 2/3, принятого за I он | рольную частицу, пропорциональна эффекту распределения ► мочевого компонента в винтовом канале шнека. Поэтому величина деформации / |д_2 названа им степенью смешения.
Несколько иной подход применен в работе (55), где при расче - н* деформации сдвига учтено наличие циркуляции в поперечном направлении винтового канала. За исходное уравнение в указанном работе принято выражение, связывающее толщину полос с деформацией сдвига (уравнение (2.234)|.
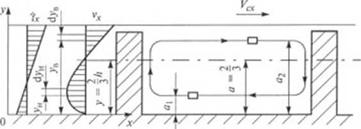
Наличие циркуляционного потока в винтовом канале приводит юму, что любая частица, движущаяся через нижнюю область в положении в|, оказывается в верхнем положении а2 (рис. 2.57), а шачения а, и а2 связаны очевидным кинематическим соотношением:
о, 1
vx(a2)da2. п.265)
О а, 4
( учетом выражений для ух (см. раздел 2.7) получим:
я2-a* =aj-a?- (2.266)
Чля определения деформации сдвига авторы работы |55| рас - • м. привали циркуляцию жидкости в поперечном направлении. 13 результате проведенных исследований установлено, что де-
|
Рис. 2.57. К расчету смесительного вотдействия при экстру тин |
формация сдвига в поперечном винтовому каналу направлении равна
Г =_______ -_____ J
х /»(l-tp)cosa г'
а деформация сдвига вдоль винтового канала составляет:
L
Г. =
; /isina*
В этих выражениях
|
rcz. |
Т _dvi*
1 х -
da, vf* vx ’
|
dvv |
|
(2.267) |
dv2td a2 da2 dv,.
|
f dv’2x |
da2 |
c. > |
|
|
a=0V d°2 |
da, |
da, J |
|
|
а к? X 1 |
<bvx |
|
*2х+а л '-укТ^-^Т^ da2 da, da, " da, |
|
Wx-Wlx |
|
здесь a,, ~ координаты частииы в нижнсй и верхней частях винтового канала; vu. vz* “ скорости частиц жидкости с координатами alt а2; vx — средняя скорость циркуляции рассматриваемой частицы жидкости. |
|
(2.268) |
|
tga 1 - a |
|
Г = Гх sin a + Г, cosa = — * li |
|
Если известны Тх и Tz для данных значений а, то нужно подставить значения некоторых переменных, чтобы выяснить влияние на суммарную деформацию сдвига угла наклона винтовой ли- |
Суммарная деформация сдвига
ими «, отношения обратного потока к прямому <р и глубины кана-
i. i Л.
Аналогичный подход при анализе процесса смешения в зоне до - шрования одношнскового экструдера использовал и Д. М. Мак - Келви |4].
По аналогичной методике Р. В. Торнер |5| с учетом аномалии ия (кости экструдируемого материала (псецдопластичной жидко - сги) получил уравнение для расчета Гх и Г..
Общий недостаток, присущий работам"(4, 6, 48, 55J, состоит в mi порировании поля скоростей сдвига по высоте винтового кана-
1.1. что может привести к ошибочному выводу о действительной 1с<|юрмаш1И сдвига. Излагаемый ниже подход свободен от этого недостатка и позволяет получить математическую модель процесса смешения, обладающую более высокой степенью адекватности.
|
г = |
Из рассмотрения поведения элементарного куба, выделенного и ( расплава полимера, на гранях которого действуют силы сдвига и двух взаимно перпендикулярных направлениях, получена зависимость между толщиной полос г и деформациями сдвига Гх и /'. 146, 66, 67]:
(Гх + Г()ч (2.269)
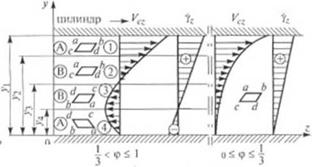
При выводе расчетных уравнений учитывали изменение направления скоростей сдвига как вдоль, так и поперек винтового капала (рис. 2.58). Распределение линейных скоростей полностью описывается уравнениями (2.64) и (2.69), а выражения для скорости сдвига иух можно получить дифференцированием указанных уравнений по у
dv. vc, (l-Зф + бшр)
11ри этом в плоскости yoz величина и направление сдвига зави-
* Mi от параметра <р. При ф < 1/3 отрицательная область на эпюре
исчезает, а при <р = 1 (полностью закрытый выход) она максима и, на. На эпюру ух параметр ф не влияет.
благодаря наличию циркуляционного потока в плоскости элементарные частицы полимера при своем движении по винтовому » аналу периодически попадают в области с различными направлениями сдвига как в плоскости yoz, так и в плоскости хоу. При рас - . могрении сдвига в направлении оси <: необходимо выделить два
• Iччая: 1 > ф > 1/3 (наличие отрицательной области сдвига по вы - < «не канала) и 0 < ф £ 1/3 (направление сдвига по высоте канала не меняется).
Действие различною но высоте канала направления сдвига в плоскостях хоу и yoz рассмотрим на примере деформации [рани элементарного кубика (см. рис. 2.58). Винтовой канал по высоте условно разобьем на четыре зоны: 1—4 — в плоскости yoz и I—IV — в плоскости уох. Как видно из рис. 2.58, направления сдвига в зонах /, / и /К 4 противоположны, а в зонах //, 2 и III, 3 — совпадают. Следовательно, при попадании частиц из зоны /, / в зону /К 4 за счет циркуляционного потока в плоскости уох деформация сдвига может полностью или частично сниматься противоположно направленным сдвигом зоны /К 4.
Для анализа процесса смешения необходимо найти координаты указанных зон, для чего обратимся к соотношению (2.266). При этом предполагаем, что любая частица, движущаяся через нижнюю область в положении в|, находится в верхней области в некотором дополнительном положении «2-
|
^//7777///////////////////////У/////////////77/7////// б IIIIICK |
|
Рис. 2.58. Эпюры линейных скоростей и скоростей ситнга и винтовом канале юны дотировании |
Уравнение (2.266) можно решить только численным методом, что усложняет инженерные расчеты. Параболическую кривую /.
|
|
|
шнек |
|
цилиндр |
|
У |
построенную по уравнению а2
< > Н(\ vmi’im г тпиипгткт пп ГО
|
|
|
0.8 |
|
0.2 0.4 0.6 а, |
(.’.266), можно с точностью до ' V аппроксимировать прямой 2 (рис. 2.59), описываемой уравнением а2 - I — ка{ или
у „л ah-kY, vt4, (2.271)
|
|
|
Границы третьих и четвертых ЮН ЛеГКО НаЙГИ, приравнивая рНС - 2.59. К определению координат IIV ПО линейные скорости и СКО - юн сдвига рости сдвига (см. рис. 2.59): |
|
(2.272) |
| лс к ■ 0,45.
тссь 1/3 < <р <, 1.
Расчет сдвига в плоскости yoz проводим для двух режимов ранты экструдера.
|
|
I. Режим работы при 1/3 > ф > 1. При известных координатах ), можно рассчитать средние скорости сдвига в указанных зонах < пш а винтового канала. Средние интегральные скорости сдвига в них зонах рассчитываем по формуле:
(2.273)
Интегрированием этого уравнения в указанных выше пределах находим выражения для средних скоростей сдвига по зонам 1—4:
|
|
Деформации сдвига элемента жидкости в плоскости yoz можно рассчитать как произведение указанных средних скоростей в зонах сдвига и времени пребывания в них частиц полимера:
|
(2.275) |
Tf^yftiNA; 2liB
= ^4=^4 na
здесь О ■ И'ф'| характеризует время пребывания частиц полимера и зонах
елнига в течение одной циркуляции; NA, Nt — числа циркуляций в областях А и В.
Для учета влияния отрицательного сдвига на общую дс<|юрма - цию в рассматриваемой плоскости винтового канала указанные выше зоны объединены в две условные области А и В (см. рис. 2.58). В области В, включающей зоны 2 и 3, сдвиг происходит в одном направлении, а в области А (зоны / и 4) — в разных направлениях; поэтому
|
(2.276) |
Числа циркуляций NA и NB можно найти из рассмотрения винтового движения жидкости в канале шнека:
|
(2.277) |
|
,7; |
tV{Z +/4V4
где t. z - длина винтового канала в зоне дозирования шнека.
Средние интегральные скорости циркуляционного потока в зонах сдвига в плоскости yoz равны
V = „ f {у)*У - (2.278)
Vi ~ У" I Ум
откуда после интегрирования с использованием пределов (2.272) получим:
|
vf |
|
(2.279) |
|
к + 2 |
|
v/ = vc |
|
v; |
|
Зф li Зф Л Зф | Зф |
Средние интегральные скорости потока в направлении оси z винтового канала находим аналогичным образом:
|
vhvcz |
|
(2.281) |
KI'M'-il ч-*К)Н
’-'■M'-rIH
Совместным решением уравнений (2.274)—(2.281) получим выражение для деформаций сдвига и Ггв, усреднение которых по
высоте винтового канала позволит рассчитать сдвиг в плоскости
vug
яф-ф,(ф) = — Ф-(ф),
A n' Asina '
I ie
ф (ф) 1-Ш-0,78фТ-22.49Ф2-16,45ф3 { ; 0,65 + 15,54ф + 37,25ф2 - 53,44ф3
|
(2.282) |
^ 1,56 + 5.17ф + 5,73ф2+2,1 1ф~'
-1,02 + 18,85ф-9,65ф2 -5,63ф3
Режим работы при 0 < ф < 1/3. При таких режимах работы •в рвччного пресса скорости vs по координате у высоты винтово - |ч канала направлены в одну сторону. В этом случае необходи
|
и верхнюю |
"• рассмотреть две области: нижнюю I <-Л
<h j. т c области с различными направлениями скорости vx. Средние интегральные скорости в этих областях:
|
-lq> |. |
|
_ v« |
|
(2.283) |
|
|-тф ; vr - |
Средние интегральные скорости сдвига в указанных областях находим аналогичным образом из выражения (2.270) для :
V-
|
(2.284) |
Ун=-^(|-ф); Тв =-^-(и2ф)
Для расчета сдвига в плоскости yoz при 0 < ф ^ 1/3 необходимо найти время пребывания частиц полимера в нижней и верхней областях за одну циркуляцию и число циркуляций:
W
(2.285)
где средние интегральные скорости v* и vBr получим из выражения для vx:
|
-х 4 V„ =-^сх- |
|
-х 2 V,, = — V, |
|
(2.286) |
|
СХ ’ |
Число циркуляций:
|
JV_ =--- 5-- |
|
tgcx. |
|
(2.287) |
|
8 I 3 5-9фИ' |
|
(2.288) |
Суммарный сдвиг в плоскости yoz находим усреднением сдвига в нижней и верхней областях по высоте винтового канала:
= т1 Mi Nih* 4i 'i N. j, h j = — • 2 ■
Методики расчета деформации сдвига в плоскостях хоу и yoz аналогичны. Однако задача упрощается тем, что координаты границ зон сдвига (см. рис. 2.58, о) не зависят от параметра ф, т. с. от режима работы экструдера. Для расчета деформации сдвига необходимо, таким образом, найти средние значения линейных скоро стей и скоростей сдвига в указанных на рисунке зонах, а также время пребывания частиц полимера в зонах сдвига и число циркуляций.
Средние интегральные скорости v* в зонах /—/Кнаходим ана - ин ично определению vf из уравнения (2.64) с использованием и|к.*дслов (2.262):
|
** = Y~y~j v*(r)dK» (2.289) ч '/+1 Уы • и куда после интегрирования получим
|
|
|
|
Значения средних интегральных скоростей сдвига в тех же зонах находим аналогично определению у?: |
|
(2.291) |
|
|
|
Время пребывания элементарной частицы в зонах сдвига I—IV м одну циркуляцию: |
|
0,828vCJt |
Число циркуляций для областей сдвига С и I) рассчитываем так к - как и для областей А и В, различие состоит в том, что в выра - м-пия для Nc и Nd входят средние интегральные скорости г>, |мч читанные для зон I—IV. Методика расчета этих скоростей ана - и'шчна расчету средних скоростей для зон 1—4 (см. рис. 2.58, а). < ргдпие интегральные скорости в зонах I—IV равны:
г, г = vcz(0,955-0,127Ф); v2 = (0,788-0,498<p);
5?И = (0,5-0,723ф); v,2v = Vf5(0,166 - 0,389Ф).
|
|
Гаким образом, число циркуляций для областей С и D:
(2.294)
Деформации сдвига в рассматриваемых областях рассчитываем как произведение скорости сдвига на время пребывания в них частичек полимера за Л'циркуляций:
|
гх _ гх _ гх ' С - ‘ I 1IV |
г *73 о.
0,828 2) АЛ vf.. 2(1 - Ф)
L, vcx I (2.295)
h vcz 1-ф'
Равенство нулю /£ свидетельствует о том, что сдвиг зоны I полностью снимается равным, но противоположно направленным сдвигом зоны IV.
Общую деформацию сдвига / находим усреднением fg и /'* по высоте винтового канала:
(229б)
Учитывая, что vcx/vc. = iga, a Lz = /./siпа, получим:
Г i I, ЛО I
ГX = *"7 I»08:------- » (2.297)
Л cos а 1-ф ' '
где L — длина зоны лозироиания по оси шнека.
Анализ полученных уравнений показывает, что при ламинарном смешении деформация сдвига в винтовом канале шнека зависит от параметра переработки ф, высоты канала А и угла наклона винтовой линии а. Таким образом, при известных г„ и /’можно рассчитать толщину полос в готовой смеси или подобран» режим переработки при известной конечной толщине полос г.
Обычно при конструировании одношнековых экструдеров заданными являются производительность машины, частота вращения шнека и его диаметр. Мри этом требуется рассчитать оптимальные геометрические характеристики шнека или подобрать параметры процесса переработки при заданном шнеке.
Аналитическое описание процессов смешения в зоне смесительных элементов шнека можно провести по аналогичной методике; подробно оно изложено в работе |57|.
Суммарная величина деформации сдвига, накопленная элементом жидкости за время его пребывания в зоне дозирования од - нош искового экструдера, равна:
Г = ГХ + Г.. (2.298)
Деформация сдвига рассматривается в данном случае как аналог работы, затрачиваемой на смешение. Поэтому применение скалярною сложения не противоречит существу рассматриваемого
m процесса. Во всех остальных случаях необходимо произвести i юление векторных величин.
Согласно уравнению (2.248) при двухосном сдвиге характерис - шка смеси у обратно пропорциональна сумме деформации сдви-
i. i в двух взаимно перпендикулярных направлениях. Следовательно. в рассматриваемом случае имеем:
I) для режима работы экструдера 1/3 < <р < 1:
3 3
|
(2.299) |
г = —
|
<Мф) |
1,08 |
|
|
т*51 /, |
sina |
cosa(l - ф) |
I к* Фг(ф) представ.1 яется выражением (2.282);
2) для режима работы экструдера 0 < <р < 1/3:
г =
|
1.08 |
|
(2.300) |
2 5-6ф____________________
sina5-9<p cosa-(l-<pj
Анализ последних уравнений показывает, что при ламинарном » мешении качество смеси, характеризуемое относительной тол - тиной полосы г, зависит от геометрии шнека в зоне дозирования (ыубины канала Л. длины зоны дозирования L и угла подъема шипового канала) и параметра) = Q/Qj (коэффициента лроссс-
III роил ния).
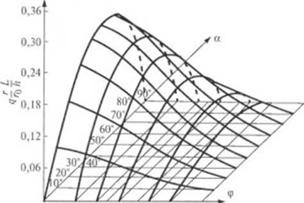
Ма рис. 2.60 в пространственной системе координат представ - 1СПО семейство кривых, показывающих влияние угла подъема а и
|
0 0.2 0.4 0.6 0,8 1.0 Гм. 2.60. Влияние геометрии шнека и параметров экструзии на качество смеси |
коэффициента дросселировании ф на безразмерный комплекс
г L
(1~Т> характеризующий качество смеси.
Y о "
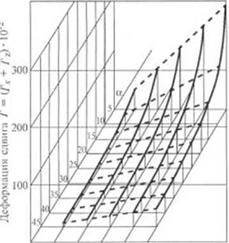
Увеличение относительной длины зоны дозирования одношнс - кового экструдера (достигаемое как увеличением длины шнека L. так и уменьшением глубины канала) приводит к росту смешивающей способности одношнекового экструдера (рис. 2.61).
Однако большие значения /.//», благоприятно сказываясь на процессе смешения и производительности, могут привести к значительному перегреву перерабатываемого материала за счет интенсивного диссипативного тепловыделения и перерасходу мощности привода.
Уменьшение угла подъема винтового канала (см. рис. 2.61) приводит к резкому увеличению смешивающей способности. Стабилизация значений / наблюдается на участке а = 15+20*, после чего значения /; почти не изменяются. При выборе оптимальных значений угла подъема а винтового канала необходимо принимать во внимание также то, что увеличение угла а подъема винтовой линии канала уменьшает производительность экструдера (см. уравнение (2.73)|.
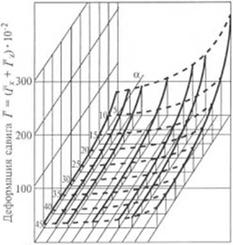
На рис. 2.62 показана зависимость суммарной деформации сдвига Г от коэффициента дросселирования <р = Qp/Qo, являю-
|
0 100 200 300 400 500 Относительная длина зоны дозирования. l./h Рис. 2.61. Зависимость суммарной деформации сдвша (тт длины зоны дозирования (<р = 1/3) |
|
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.S 0,9 Коэффши1е1гт дросселирования ф I'm-. 2.62. Зависнмосп. суммарной деформации сдвига от коэффициента дросселирования <? и угла подъема винтового канала cl /./А = 200; А = 0.5 см |
un i ося технологическим параметром работы одношнскового эк - v Фудера. Из этого графика видно, что при <р = 0 (полностью от - г рытый выход) /’ = /тах, а при ф = 1 суммарная деформация
• жига / —>«>. Однако реальные экструдеры работают при ироме - I уточных значениях 0 < ф < 0.6.
Из рис. 2.62 видно, что на участке 0 < ф < 0,6 наблюдается плавное увеличение смешивающей способности одношнековых экструдеров, а затем при 0.6 < ф 5 1 — резкое ее увеличение до бесконечности. Отсюда следует важный для практики вывод: при раною в режиме ф <, 0,6 небольшое изменение коэффициента (росселирования приводит к резкому увеличению смешивающей ■ юсобности экструдера. При этом такое изменение ф не сказываем на производительности экструдера.


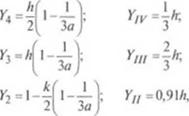
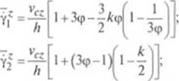
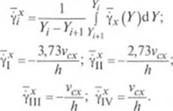
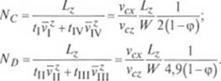
 Опубликовано в
Опубликовано в