МЕХАНИКА НЬЮТОНОВСКИХ ЖИДКОСТЕЙ
 13 ноября, 2013
13 ноября, 2013  admin
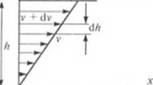
admin Рассмотрим тонкий слой жидкости, заключенной между двумя бесконечными параллельными пластинами, одна из которых неподвижна, а к другой приложено сдвигающее усилие /-’(рис. 1.2, а). Верхняя пластина под действием силы Сбудет сдвигаться относи - 1слыю параллельной ей неподвижной плоскости со скоростью v, постоянной до тех пор, пока сила /'неизменна. Поскольку даже пссмачивающая жидкость прилипает к ограничивающей ее стенке гак, что прекращается движение жидкости относительно стенки, жидкость у нижней пластины имеет нулевую скорость, тогда как - корость ее у верхней пластины равна v и совпадает по направлению с действием силы. Так как в стационарных условиях сдвигающая сила передается равномерно через жидкость к нижней плос-
|
17 |
|
) |
4 МО
|
Подвижная /^/скорость^/У/ |
|
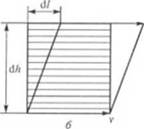
Рис. 1.2. Течение жидкости между плоскоиарахкмьиычи пластинами (а и б — см. текст) |
|
|
|
4Z22 |
|
v + d V' |
|
|
|
F77/^LLi////A |
кости, каждый слой жидкости в пределах пространства высотой /; будет перемешаться относительно следующего слоя так, что изменение скорости в зависимости от расстояния между ними (градиент скорости) будет постоянным.
Математически отношение между напряжением сдвига и вызываемым им изменением градиента скорости (поскольку dv/d/i постоянно и равно v/h) может быть выражено одним из следующих уравнений:
|
F р dv T = M“jT» d/i |
|
(1-6) (1.7) |
где I — напряжение сдвига; S — плошалi. поверхности пластины; р — коэффицм - ент пропорциональности (ньютоновская вязкость).
Уравнение (1.7) можно записать и в другом виде. Для этого рассмотрим элемент жидкости высотой d/;, вырезанный из слоя жидкости, заключенной между двумя бесконечными плоскостями (рис. 1.2, б).
В случае идеальной ньютоновской жидкости изменение деформации происходит во времени. За время d/ это изменение равно расстоянию, на которое передвигается верхняя пластина |7|:
|
(1.8) (1.9) |
d/ = (v + dv)d/-vdv = dvd/.
Дифференциал деформации сдвига г/у равен:
dv d/
, d /
dY = -77 d/i
d/i
Деля обе части выражения (1.9) на d/, получим:
С учетом выражения (1.10) уравнение (1.7) приводится к виду:
|
т = ру- |
(III)
Ньютоновская вязкость ц зависит только от температуры и дав - 1Сния и не зависит от скорости сдвига у.
График зависимости напряжения сдвига от скорости сдвига — гак называемая кривая течения — для ньютоновской жидкости представляет собой прямую линию с тангенсом угла наклона р. )га единственная постоянная полностью характеризует жидкость. Все газы, жидкости и растворы с относительно низкой молекулярной массой ведут себя как ньютоновские жидкости в пределах достижимой точности эксперимента. Все расплавы и растворы высокополимеров относятся к неньютоновским жидкостям.
Уравнение (l. l I) является частным случаем применения к илоскопараллельному сдвигу общего реологического уравнения ньютоновской жидкости. Оно может быть записано в виде:
|
! it* к — коэффициент объемной вязкости; ц — коэффициент вязкости при сдвн - и1вом течении. |
Компоненты Ду тензора скоростей деформации Д и 5;, единичного тензора 6 определяются следующим образом:
|
|
6/j = 0, если / * j = I, если /' =j.
|
|
не между х, у, z и системой индексов I, 2, 3 существуют следую щие соотношения:
X, = X, *2 = У, х} = г.
В частном случае, когда / = 2 и у = 1, уравнение (1.12) примет
|
или в системе индексов х, у, z: |
|
|
вид
|
|
Заметим, что если бы vy было равно нулю, как при плоскопа - раллельном сдвиговом течении, то уравнение (1.13) упростилось бы:
Математическая формулировка задачи течения всегда приводит к системе уравнений, состоящих из реологического уравнения, уравнений неразрывности, движения, энергии и уравнения состояния жидкости. Решением задачи являются функции, удовлетворяющие этим уравнениям и определенным граничным условиям.
Для упрощения постановки задачи ньютоновского течения ниже приведены скалярные уравнения (1.12) в прямоугольных, цилиндрических и сферических координатах.
Прямоугольные координаты (х, у, z)'-
Цилиндрические координаты (г, 0, z):
T1»=+M[2(^+^)'f(v'v)]+x(v‘');
+ K(Vv);
|
rA( vr V 1 dvr drl r I г Э0 |
TK=+p
|
Эу0 |
|
|
dz |
г ЭО ] |
|
+*ь) |
|
|
Эг |
Эг ’ |
=4r = +H *0:=*гО = +И V=T/t =+V
-ч1э, , i3v0 Ov.
(v-v) = -—(rv,)+—-ii + — v ' rdrK r> гЭе dz
Сферические координаты (г, 0, ср):
|
V = +Р %> = +И |
2^-f(Vv)]+s(Vv);
Хй^НН»™
|
sinO Э |
S 1, 1 Эу0 |
|
г ЭО |
sin0 1 rsinO Эф |
|
с) f V0 Л 1 dvr г— — 1+ - дг[ г г ЭО |
|
1 dv. Э - + г—- |
|
_ф г |
|
trt)=T0r =+й *Оф=тфв =+И V=T«p = +>4 I э |
|
rsinO Эф дг I Э |
(V - v) = -!r—(/2vr) + ———(v0sinG) + —?—
г2 дЛ ' rsinO ЭО rsinO Эф
Решение простой задачи ньютоновского течения иллюстрируется примером 1.1 111.
Пример 1.1.
В этом примере рассматривается установившееся ламинарное осесимметрическое течение несжимаемой ньютоновской жидкости через длинную трубу круглого сечения радиусом R. Температура стенки трубы Tw поддерживается постоянной. Задача состоит в отыскании распределения скорости и температуры в поперечных сечениях трубы, настолько удаленных от входа, что ни температура. ни скорость не зависят от продольной координаты Z - Для простоты предполагается, что вязкость р постоянна.
|
|
В этой задаче все производные температуры, скорости и компонентов девиатора напряжений по переменным 0, г и / равны нулю, компоненты скорости v0 и v, равны нулю, и, вследствие того, что жидкость несжимаема, (Vv) = 0. Уравнения движения и энергии (см. с. 14—16) принимают следующий вид:
(1.14)
(115)
|
|
|
дР pdf dv. — = г— : |
|
Эг г дг дг |
|
/ |
Вводя в эти уравнения выражения для (см. выше) и q„ (см. табл. 1.1), получим:
(1.16)
|
|
Граничные условия этой задачи:
(1) v,(/?) = 0; (3) vj(0)=0,
(2) Г(/?) = ГИ; (4) 7"'(0) = 0,
Вследствие того, что левая часть уравнения (1.16) не зависит от г, его можно непосредственно проинтегрировать. В результате получим:
Из третьего граничного условия следует, что постоянная интегрирования С| равна нулю.
Распределение скорости, полученное при интегрировании уравнения (1.18), представляется выражением
которое при определении С2 из первого граничного условия и последующей подстановке в уравнение принимает вид:
|
-й |
|
tf_dP 4ц Эг |
|
v. = — |
|
(1.20) |
|
'Знак «минус» указывает на то, что жидкость течет в направлении уменьшения давления. Распределение температуры можно получить подстановкой равенства (1.18) в выражение (1.17) и интегрированием последнего. После первого интегрирования получим: 2 _3 |
|
Л dP |
|
дТ А_1 О Г Г Г" [ Ly |
|
(1.21) |
|
Эг 4цк dz I 4 г |
причем из четвертого граничного условия следует, что постоянная интегрирования С3 равна нулю. Интегрирование уравнения (1.21) дает выражение
4р*|ч dz ) 16 4’
которое при определении Q из третьего граничного условия примет вид:
|
(1.22) |
|
К |
64 ц/; I dz
Скорость жидкости на оси трубы v. |г=,0 = v0 выводится из уравнения (1.20):
R:dP
5Г»
4ц dz
а температура жидкости на оси трубы, рассчитанная по уравнению
11. 22), определяется выражением:
Г R*A(dP^ _4*Ур 64ц*| dz I 4*
ньютоновского течения через длин
|
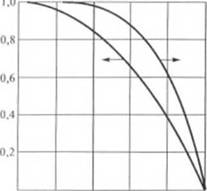
Tw F’hc. 1.3. Распределение безразмер- |
|
|
|
y ных скоростей и температур для И IILUtmitfinrL'nrn Н1>П1< 1 iluu. |
|
|
|
() s Если, например, скорость жидкости на оси трубы равна 0,1 м/с, вязкость жидкости о. б равна 104 пз (1()? И с/м2), а |
|
коэффициент теплопроводности — 10 3 калДсм • с • град) <М (0,419 Вт/(м ■ град)], то тем |
|
пература жидкости на оси () 2 трубы будет на 6 °С выше, |
ную трубу
чем у стенки грубы.
Разделив выражения (1.20)
и (1.21) соответственно на v<j
о 0.2 0,4 о. б 0,8 r/R и 7q — Tw, приведем их к без-
SHAPE * MERGEFORMAT

|
размерному виду: |
|
|
На рис. 1.3 показана зависимость этих безразмерных переменных от безразмерной координаты r/R.

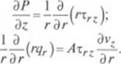
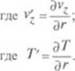
 Опубликовано в
Опубликовано в