Температура стеклования Тс многих статистических сополиме­ров хорошо описывается экспериментальной формулой вида

7’c = ®i7’ci + ®2^c2—(2.24)

Здесь TGi — температуры стеклования; ш* — весовые доли компо­нентов; ф— параметр, значение которого зависит от вида компо - - нентов и не зависит от их содержания в системе и который опреде­ляется энергией взаимодействия компонентов. Данная формула может быть обоснована теоретически [2.5]. Ее можно использовать. также для оценки энергии взаимодействия компонентов в различ­ных полимерных системах, для которых может быть установлено значение параметра ф.

Известно, что тепловое расширение полимеров при температу­рах выше Тс происходит значительно быстрее, чем при температу­рах ниже Тс. Отличие коэффициентов объемного расширения поли­меров легко объяснить, если предположить, что увеличение их объ­ема при температурах выше Тс происходит за счет двух факторов: озрастания амплитуды ангармонических колебаний и увеличения полимере вакантных мест — дырок. Ниже Тс из-за большой вяз - ости системы изменения количества дырок в ней не происходит и асширение полимера осуществляется лишь за счет увеличения амплитуды ангармонических колебаний. Для разных полимерных истем Тс характеризуется определенной объемной долей дырок, ли долей свободного объема, равных 0,025, при температуре Т = Тс. Известно, что объемную долю ср дырок в системе при произ - ольной температуре Т можно оценить по формуле

<Р = ехр[—е/(АГ)], (2.25)

де е — энергия образования дырок; k — постоянная Больцмана, то соотношение применимо для расчета объемной доли дырок в нтервале температур выше Тс. Поскольку Тс является нижней раницей этого интервала, формула (2.25) применима и при Т =

Энергию образования дырки можно рассчитать, воспользовав - ись решеточной моделью полимерного раствора. Допустим, что в истеме имеется п дырок, каждая из которых занимает одну ячей - 7. Число ячеек, занятых первым компонентом, обозначим через 1, а вторым — через я2. Компоненты могут входить в одну молеку - у, образуя сополимер, или входить в разные молекулы, когда име - ся смесь двух полимеров. Учитывая это, для общности рассмот­рим два случая — случай статистических сополимеров и случай гомогенных смесей полимеров. У дырок в системе имеется nz кон­тактов (г — координационное число решетки), у первого компо­нента rii(z—2), а у второго ti2{z—2) контактов. Наличие сомно­жителя (z—2) объясняется тем, что вокруг каждой ячейки, заня­той тем или иным компонентом, имеются две ячейки, занятые соседями по цепи. Используя атермическое приближение, т. е. пола­гая, что как в статистических сополимерах, так и в гомогенных сме­сях полимеров компоненты и дырки распределены в системе слу­чайным образом, получим, что энергия £ системы с дырками долж­на определяться выражением

n(z — 2)бц. nl(z— 2)s22 П! П2(2 — 2)е12

С.---------------------------------------------------------------------------- = 1 ,

2(Л! + П2 -{- п) 2{П - Ь п2 + п) П1+П2+П

где 8ц, 812, 622 — энергии взаимодействия компонентов 1—1, 1—2 и 2—2 в расчете на один контакт. Если считать, что число дырок п равно нулю, то из этого выражения можно получить соотношение для энергии системы без дырок. Вычитая энергию системы без ды­рок из энергии системы с дырками и разделив на число дырок, получим энергию образования дырки:

4(z — 2) £22(^ — 2) , Д Е

• = —"Pi -*> ! —к'

где AE=x!2Na{z—2)(ец + 822—2ei2). Здесь фЬ ф2— объемные доли компонентов в системе; NA— постоянная Авогадро. Величина, рав­ная 2Д£, представляет собой энергию, которая выделяется (Д£>0) или поглощается (Д£<0), когда рвется по NA(z—2) контактов ти­па 1—1 и 2—2 и вместо них образуется 2NA(z—2) контактов типа 1—2. Подставляя энергию дырки в выражение (2.25), записывая его для Тс, логарифмируя и разрешая относительно Гс, получим

TOC o "1-5" h z 'Г — 2) I £22(^—2) Д£

Т — ср.—iil------------------------- i----- - L. m —£±Ь----------- L------ cp2cp2------------------------------ .

2k In 0,025 1 2k In 0,025 In 0,025

Если в этом выражении положить ф1 или ф2 равными нулю, то щ{г—2)/(2Ып 0,025) и 822(z—2)l(2k In0,025) можно выразить че­рез Тс соответствующих компонентов. Далее, вычислив In 0,025 и введя вместо NAk молярную газовую постоянную R, окончательно получим

7’с=?1П1+%7,с2+0.271 (2.26)

Параметр АЕ здесь является константой, зависящей от природы компонентов, но не от содержания их в системе, и характеризует энергию взаимодействия компонентов. Если Д£=0, то Тс полимер­ной системы аддитивно складывается из температур стеклования отдельных компонентов. Если Д£>0, т. е. когда разрыв контактов типа 1—1 и 2—2 требует затраты меньшей энергии, чем ее выде­ляется при образовании двух контактов типа 1—2, то величина Тс больше аддитивной. Наконец, если Д£<0, т. е. когда разрыв по

дному контакту типа 1—1 и 2—2 требует большей энергии, чем Не выделяется при образовании двух контактов 2—2, Тс меньше ддитивной.

Поскольку плотности большинства полимеров близки, выраже - ия (2.24) и (2.26) практически мало отличаются друг от друга, ’з сравнения этих соотношений следует, что роль параметра ф грает величина —0,271A£yi?.

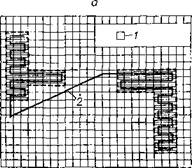
Перестраивая зависимости Тс в функции от объемной, а не ве- ’ овой доли одного из компонентов, можно из полученных графиков пределить величину АЕ для данной системы. На рис. 2.11 в ка - естве примера приведены зависимости Тс некоторых сополимеров

Рис. 2.11. Зависимость тем пературы стеклования Тс не ;которых статистических сопо лимеров от их состава:

— метил акрилат-стирол (Ст), б — етилакрилат - метилметакрилат (ММА), в — винилацетат-винилхло ‘ (ВАВХ)

т объемной доли одного из компонентов. Точками здесь показаны экспериментальные данные, а сплошные кривые построены соглас­но уравнению (2.26) в предположении, что для сополимера мети - лакрилат-стирола А£=0, для метилакрилат-метилметакрилата

А Е = 600 Дж/моль и для винилацетат-винилхлорида АЕ =

•=—1780 Дж/моль. Экспериментальные точки сравнительно непло­хо ложатся на теоретические кривые. Небольшие расхождения мо - ~ут быть связаны с ограниченной применимостью использованного* опущения о случайном распределении в системе компонентов и ырок. При значительных отличиях АЕ от нуля при его положи- ельных значениях вероятность размещения различных компонен - , ъ по соседству друг с другом будет увеличиваться, а вероятность бразования дырок в тех местах, где таких контактов двух компо - ентов больше, будет уменьшаться. Наоборот, если АЕ велико и “рицательно, вероятность размещения различных компонентов па оседству друг с другом будет уменьшаться, а вероятность образо- ания дырок в местах, где таких контактов больше, будет увели - иваться, ибо образование их в данном случае потребует меньшей нергии.

Таким образом, можно сделать вывод, что уравнение (2.26) “довлетворительно описывает отклонение Тс от аддитивности и его южно использовать для оценки энергии взаимодействия различ - ых компонентов статистического сополимера и гомогенной смеси олимеров друг с другом.

Следует отметить, что в статистических сополимерах могу* Меть место значения величины АЕ и положительные (например, ■ля стирол-бутадиена) и нулевые (например, для метилакрилат- тирола).