ОСОБЕННОСТИ РАСПРОСТРАНЕНИЯ ЭЛЕКТРОННОГО ИЗЛУЧЕНИЯ В ПОЛИМЕРНЫХ СЛОЯХ
 17 января, 2014
17 января, 2014  admin
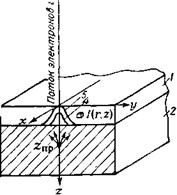
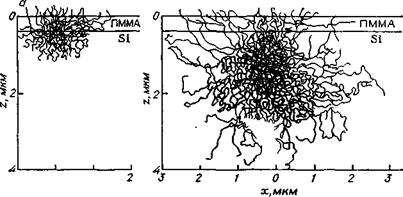
admin В потоке электронов отдельные частицы взаимодействуют друг с другом [4]. Рассеяние электронов ведет к распространению электронного излучения по всем направлениям. Следовательно, и элек - тронорезист (рис. VII. 1) экспонируется в тех местах, куда первоначально не направлялся пучок электронов. Поток электронов в слое резиста делят на излучение, сохраняющее направление первоначального пучка, и обратно отраженное электронное излучение. На рис. VII. 2 показаны рассчитанные методом Монте-Карло траектории 100 электронов в слое резиста на подложке при разных ускоряющих напряжениях. Хорошо заметна доля электронов, имеющих направление первоначального пучка, и рассеянных. При 10 кВ рассеянные электроны расходятся на расстояние около 1 мкм, а при 20 кВ —уже на 3—4 мкм.
Энергия, рассеянная в единице объема одним электроном /(г, z) (где г — радиус отклонения электрона при прохождении вертикального отрезка z), зависит от атомного номера элемента, атомы которого входят в состав вещества поглощающей среды, толщины подложки и слоя резиста, а также скорости падающих электронов (ускоряющего напряжения). Экспонирование резиста в местах, куда не падает первоначальное излучение, называется эффектом близости и ведет к значительным ограничениям формы Zn =£)
|
Пр |
|
|
Рис. Vll. 1. Пространственная модель рассея - Х иия пучка электронов нулевого диаметра в слое резиста на толстой подложке:
/ — резист; 2 — подложка; 3 — обратное отражение из подложки; 4, 5 —профиль распределения обратного отражении в объеме слоя резиста (5) и в подложке (4); zn — глубина проникновения пучка электронов.
и размеров элементов рельефа, которые можно получить с помощью данного резиста [5]. Этот эффект, наблюдаемый главным образом у высокоразрешенных рельефов при толщине слоя резиста менее 1 мкм, стимулировал интенсивное теоретическое и экспериментальное излучение распространения электронов в резисте на
|
<5Г
О 1 X, мкм Рис. VII. 2. Траектории 100 электронов в ПММА на кремнии по осям х и z (см. рис. VII. 1), рассчитанные по методу Монте-Карло при ускоряющем напряжении 10 кВ (а) и 20 кВ (<?). |
подложке. Было предложено несколько моделей, позволяющих предсказывать экспозиционные профили в резисте и, следовательно, осуществлять выбор оптимальных параметров для получения требуемого размера элементов и толщины рельефа. Моделирование дало также возможность определять влияние отдельных параметров экспозиционного оборудования, природы резиста и подложки, а также формы рельефа.
Основными параметрами, необходимыми для определения формы профиля, являются плотность поглощенной энергии Е (г, z) и ее распределение в слое резиста. Для наиболее простого случая стационарного электронного излучения, характеризующегося потоком электронов г, падающих на слой резиста за время т, можно записать следующее выражение [6]:
(Ст/е) / (г, г) = Е (г, г) (VII. 5)
где E(r, z) — общая энергия, рассеянная в единице объема, эВ/см8; гг/е— количество падающих на слой полимера электронов.
Предсказание профиля резиста требует моделирования экспозиции и проявления. Для количественного описания распределения энергии в полимерном слое, помещенном на подложку, наиболее часто используется метод Монте-Карло. Он состоит в моделировании траектории электронов в системе резист — подложка на ЭВМ. Взаимодействие электрона со средой представляет собой ряд последовательных отражений, при которых происходит изменение направления движения электрона и потеря им энергии. В большинстве подходов используют модель с одним отражением, направление которого случайно. При этом предполагается, что направление движения электрона изменяется в результате его упругого отражения от атомного ядра, причем угол столкновения может быть вычислен из приближенных решений уравнения Шре - дингера, предложенных Борном [7]. Угловое распределение рассеянных электронов зависит от потенциала. Чаще всего используют потенциал Томаса — Ферми, рассчитываемый в предположении, что на движущийся электрон действует атомный заряд близлежащего ядра, величина которого корректируется с учетом электронной оболочки атома. Предполагается также, что между двумя упругими столкновениями электрон движется по прямой с длиной, равной среднему свободному пути, и теряет энергию. Потерю энергии электроном обычно рассчитывают в соответствии с приближением постепенного понижения (метод CSDA) по уравнению Бете:
dE 2 пеАпе аЕ
= -Г-1п ЯГ (VIL6)
где пе — плотность электронов атома; Е„ — средняя энергия возбуждения атома; Е—энергия взаимодействующего электрона; а — константа, равная 1,166.
Другие модели используют модификацию метода CSDA для статистических расчетов неупругих столкновений. Рассеянная энергия всегда меньше начальной энергии электрона.
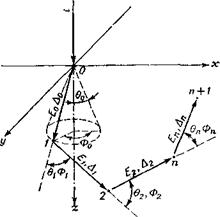
Последовательность столкновений для отдельного электрона изображена на рис. VII. 3. В начальном положении электрон имеет энергию Ео и движется под углом 90° к поверхности бесконечно толстого слоя [8]. Первое рассеяние происходит на поверхности. Углы отклонения 0О и Ф0, а также длина шага А0 вычислены по
методу Монте-Карло. Построением множества моделей (точки
1, 2, ..., п, п+1, ..., °о) получают распределение траекторий (см. рис. VII. 2) и распределение поглощенной энергии, из кото
рого можно определить величину /(г, г) для каждой точки (см. также [9]).
|
|
Для получения надежных статистических результатов при использовании метода Монте-Карло необходимо рассчитать траектории нескольких тысяч электронов, что требует большого машинного времени. По этой причине на практике для предсказания рассеяния электронов используют аналитические модели, в которых предполагается, что потеря энергии в результате рассеяния складывается из трех составляющих: рассеяния под малым углом (РМУ) из пучка в полимере, рассеяния под большим углом (РБУ) в подложке и обратного отражения (00) в полимере. Для определения РМУ в резисте используют две аналитические модели. Гринейх и Ван Дузер [10J построили свою модель на основе теории рассеяния Ленца, по которой угловое распределение рассеянных электронов определяется интегрированием уравнения Больцмана по всему пространству. В упрощенном подходе используют
Рис. VII. 3. Пути электрона в слое материала, найденные по методу Монте-Карло.
уравнение Больцмана в приближении Ферми с учетом кратных малых углов [7]. Такой подход является, следовательно, псевдо - моноэнергетическим и ограничен случаем толстого слоя резиста, когда средняя энергия электрона, проходящего через поверхность раздела, равна энергии столкновений. Эта модель дает непосредственно распределение электронов в резисте в форме функции вероятности Я:
Н (г, г) =» [31/(4пг3)] ехр (—3/г2/4г3) (VII. 7)
где / — средний свободный путь электрона, определяемый в нерелятивистской теорнн нз соотношения (VII. 8) [10]:
5,12-10~3£2Л
pz2ln (0,7257?^-['3) (VII-8)
где А — массовое число атома элемента, входящего в состав вещества резиста, в поле втйго атома находится электрон; Е — энергия электрона; р —плотность резиста.
Если столкновение электронов имеет Гауссово распределение / (Г) - i0/nr2 ехр - (гг/г2) (VII. 9)
где Т—Гауссов (среднеквадратичный) радиус распределения
то результирующая плотность распределения электронрв в твердой фазе определяется круговым интегралом (VII. 10) входной
функции I(г)' и соответствующей функции Н(г, г):
2я л
/ (г, z) = Н (г, z) 1 (г) rdr d&
О
Интегрирование уравнения (VII. 10) не может быть проведено в аналитической форме необходимо использовать численные методы.
Потеря энергии одним электроном в 1 см3 при РМУ может быть рассчитана из соотношения:
|
|
(VII. И)
Плотность поглощения энергии одного электрона рассчитывается как сумма плотностей поглощения РМУ, РБУ и ОО:
|
(VII. 12) |
I (г, г) = / (г, г)РМу + / (г, г)РБу + / (г, г)00
Общая плотность поглощенной энергии определяется как произведение /(г, г) и общего электронного тока.
|
|
|
ю~6 D, Кл/см2 |
Для расчета коэффициентов ОО существует ряд подходов. Простая эмпирическая модель для отражения [11] основана на прямом наблюдении на несколь-
ких субстратах химических изменений, обусловленных ОО при разных ускоряющих напряжениях, и приложима для анализа изменений,
|
|
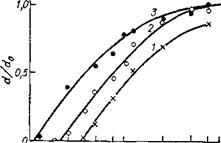
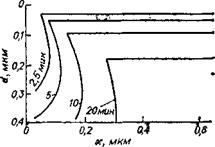
Рис. VII. 4. Кривая чувствительности негативного электронорезиста СОР на разных подложках (толщина слоя ре - знста do = 0,66 мкм, ускоряющее напряжение 20 кВ):
/ — 0,1 мкм S13N4; 2 — 0,1 мкм S13N4 на Si; 3 — 0,4 мкм Аи на Si.
происходящих при экспозиции резиста. Модель не зависит от пути рассеяния и расчета теряемой энергии.
Иной подход для эмпирической оценки ОО заключен в методе так называемого свободно стоящего толстого слоя резиста. Эта модель обсуждалась [12] с использованием кривой чувствительности негативного резиста (рис. VII. 4). Кривая, отвечающая слою резиста на подложке из Si3N4 толщиной 0,1 мкм хорошо приближается к идеальному случаю свободно стоящего слоя резиста, так как коэффициент ОО подложки очень мал (0,01—0,02).
Для данной экспозиции на большой площади, которая используется для построения кривой чувствительности, плотность рассеянной энергии электронов зависит только от глубины проникновения пучка в слой резиста znp. С учетом этого можно написать следующее уравнение [13]:
|
|
где О — экспозиционная доза (Кл/см2); длины в направлении г.
Специфическую рассеянную энергию можно найти из выражения:
dlz Я (f) иа
потеря энергии на единице
(VII 14)
|
dz |
Rc
где Ua — ускоряющее напряжение; Ra— длина пробега Грюна; Ra = [0,046/р](Уа; Я (/) — функция, связывающая znJ, с экспозиционной дозой и выраженная через нормализованное проникновение электронов f — znp/Ra (плотность р полимерных материалов приблизительно равна 1).
|
|
Зависимость гпр от экспозиционной дозы определяется экспериментально измерением степени ионизации как функции проникновения электронного пучка или его проникновения в зависимости от ускоряющего напряжения. Зави - л симость К от f можно выразить в полиномной форме:
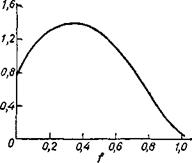
Я (f) = 0,74 + 4,7f + 8,9f2 + 3,5f3
(VII. 15)
Зависимость Я от f (рис. VII. 5) образует экстремум, отвечающий максимуму рассеяния энергии, кото-
Рис. VII. 5. Зависимость нормализованной глуби - иы проникновения электронов / от X в веществе, содержащем элемент с низким атомным номером.
рый наблюдается при конечной глубине проникновения и зависит от ускоряющего напряжения.
Специфическая рассеянная энергия имеет две компо
ненты:
dlz ( dlz ( dlz ,
лГ-Ьг)РМУ + Ы0оЛг (Vine)
|
записать |
Вводя коэффициент 00 как т = ^ /(jjz~)0o' можно
|
dlz dz |
(4г), " + ,|)
(VII. 17)
' РМУ
Для толстого слоя резиста на Si3N4, когда т] « 0, можно с использованием уравнения (VII. 10) получить соотношение:
|
dz / рму |
(VII. 18) 219
где Dlv — экспозиционная доза в точке гелеобразования на границе подложки и резиста; Е — адсорбированная на этой границе энергия электронного излучения.
Вообще для любого субстрата можно записать:
|
(VII. 19) |
4 {41е) [( dl)рму + ( dl) 0О ]
Из последних трех уравнений получаем выражение:
|
(VII. 20) |
(Djy^-l + V
где i)‘ — эффективный коэффициент ОО на границе подложки и резиста.
Эта модель, использующая зависимость глубины проникновения г от дозы излучения, дает возможность вычислить энергию Е в точке гелеобразования, зная дозу излучения в этой точке, и предсказать зависимость дозы в точке гелеобразования от ускоряющего напряжения D{ = {Ua°’75), что хорошо согласуется с экспериментом. Найденные значения т]г также согласуются с величинами, вычисленными по методу Монте-Карло [12]. Таким образом, с помощью модели обратного рассеяния можно вычислить долю 00 в любой точке простой дополнительной модификацией плотности РМУ в виде /0(1 4-г|).
Результаты, полученные с помощью аналитических моделей и метода Монте-Карло, хорошо коррелируют, из чего можно сделать несколько обобщающих заключений.
Рассеяние энергии идет по двум каналам: РМУ и 00. Энергия ОО локализована вблизи оси луча. При прохождении через резист электронный пучок в результате РМУ расширяется, так что на границе резист — подложка экспонируется площадь большая, чем в поверхностном слое резиста. Эта площадь определяется длиной пути электрона в резисте и подложке. Хотя максимальное рассеяние энергии в единице объема из-за 00 гораздо меньше, объемный их вклад сравним. Доля РМУ и 00 в экспозиции резиста зависит от энергии излучения, толщины слоя и атомного номера элемента, входящего в состав вещества подложки. При повышении энергии излучения уменьшается потеря энергии на единицу длины пути, а при увеличении толщины слоя возрастает кумулятивный эффект столкновений электронов РМУ. Площадь, экспонируемая на границе резист — подложка, увеличивается с ростом толщины слоя. Адекватное экспонирование требует, чтобы пробег электронов в полимерном слое превышал его толщину с тем, чтобы обеспечить экспонирование резиста вблизи границы резист — подложка. С возрастанием атомного номера элементов, образующих вещество подложки, увеличивается доля электронов 00 и уменьшается длина пробега электронов в подложке, в результате чего электроны 00 концентрируются вблизи оси луча.
С целью уменьшения эффекта обратного рассеяния электронов и повышения разрешающей способности разработана теоретиче
ская модель коррекции дозы электронно-лучевого экспонирования резиста. Ее применение обеспечивает получение необходимого профиля линии в проявленных резистах независимо от материала подложки [14].
|
|
Теперь с помощью моделей проанализируем проявление резиста. При экспонировании позитивных резистов уменьшается их ММ, поэтому участки с разной поглощенной энергией различаются по ММ резиста [15]. Если используемый проявитель растворяет полимер с ММ меньше критической, то проявление профиля резиста протекает в соответствии с профилем поглощения энергии Екрит [Ю]. Такой подход правомерен в случае высоких доз излучения и высокой контрастности, так как только при этом профиль резиста становится независимым от продолжительности проявления. Для ПММА на алюминиевой подложке при дозе 0,3-10-8 и 1,0-10-8 Кл/см2 наблюдается хорошая корреля-
Рис. VII. 6. Влияние на профиль края рёльефа ПММА (х— расстояние от оси дочка электронов; d — толщина слоя) продолжительности проявления в метилизобу - тилкетоне.
ция между рассчитанными [10] и найденными экспериментально профилями [16]. Модели, учитывающие скорость проявления, использовали Гатцакис [17] и Гринейх [15]. Гринейх использует эмпирически установленное уравнение для скорости растворения резиста R в экспонированных участках:
|
(VII. 21) |
Я = Я0+р/М
где #0, р и а — константы для данного растворителя; Mf—ММ в данном участке резиста после экспонирования.
Типичная картина зависимости профиля края рельефа ПММА от продолжительности проявления изображена на рис. VIE 6.
Моделирование процесса проявления негативного резиста более сложно, так как наряду с проявлением протекает экстракция растворимых веществ с экспонированных участков, набухание последних и усадка после сушки. Несмотря на это, и здесь приближенные модели дают хорошее согласие с экспериментом [13], особенно для дозы, условно локализованной в основном в пределах оси экспозиционного пучка излучения и ширины линий элементов рельефа больше 0,4 мкм.
Теоретические соотношения, характеризующие форму профиля элементов рельефа после проявления, позволяют правильно выбрать параметры обработки и дают возможность алгоритмизировать эффект близости, что важно при экспонировании через шаблон, имеющий геометрически сложные элементы [18].

 Опубликовано в
Опубликовано в