Моделирование экспонирования и проявления
 16 ноября, 2013
16 ноября, 2013  admin
admin В мировой практике до сих пор не созданы. нормы для стандартизации и унификации светочувствительности полимеров. Поэтому представляют большой интерес работы, в которых при помощи построения моделей в сочетании с новыми оценками процесса проявления предпринимаются попытки количественно описать экспозиционные характеристики фоторезистов.
Важные работы в этой области выполнены Диллом с сотрудниками [1, 35, 36, 83]. Модель построена на основе композиции позитивного резиста (AZ-1350J), образованного новолаком из крезола и формальдегида и широко применяемого замещенного нафтохииондиазида (пат. США 3201239) (см. гл. II).
Если экспонирование — оптический процесс, который изменяет компоненты фоторезиста химически, то проявление — поверхностное растворение и удаление фоторезиста со скоростью, зависящей от степени превращения ингибитора растворения.
Пленка новолака растворяется в обычном щелочном проявителе со скоростью 15 нм/с, в присутствии ингибитора—светочувствительного компонента (обычно 25—30 %) растворимость пленки снижается до 0,1—0,2 нм/с. Очевидно, отношение растворимостей иоволака без и с ингибитором растворения составляет 75—100. Свет в области 200—450 им разлагает ингибитор и вызывает повышение скорости растворенья экспонированного слоя до 100—200 нм/с в зависимости от доли неразложившегося ингибитора.
Была выбрана модель, дающая взаимосвязь не только между экспозицией и скоростью растворения (скоростью проявления), но и между этими параметрами и профилем слоя резиста. Поглощение света в слое толщиной d(d = <0, 1> является функцией молярных коэффициентов поглощения ингибитора at, новолака а2 и продуктов фотолиза а%. Авторы предположили, что доля непрореагировавшего ингибитора в момент времени t является функцией пара
метров: А, являющегося функцией поглощенного излучения; В, не зависящего от поглощенного излучения, и С, являющегося функцией светочувствительности. Параметры А, В а С являются также функциями длины волны света. Скорость проявления R зависит от химического состава резиста, величины М и состава проявителя. Для постоянных условий удалось в итоге вывести функцию R = f(M), которая описывает проявление конкретного резиста в данном проявителе.
Условием адекватности модели является однородность нанесения слоя резиста на подложку и изотропность его свойств.
На показатель преломления и абсорбционную способность слоя не должно оказывать влияние рассеяние света. В этом случае существует линейная зависимость пропускания слоя от толщины слоя резиста, что соответствует закону Ламберта — Бера. В изучаемом диапазоне длин волн актиничного света ингибитор должен заметно поглощать. Поглощение света при разложении ингибитора также должно отвечать закону Ламберта — Бера. Хотя были обнаружены отклонения от этого закона, нх относят к крайним условиям экспонирования и не учитывают при практическом использовании фоторезиста [84]. Поэтому принимают, что выполняется простое соотношение (I. 19) между количеством экспонирующего света и химическим изменением, вне зависимости от интенсивности облучения (взаимозаместимость) [85]. Для исключения отражения от подложки при моделировании в качестве подложки было использовано стекло с тем же показателем преломления, что и у резиста [па « 1,70 при 404,7 нм), кроме того, на нижнюю сторону стеклянной подложки был нанесен слой фторида магния MgF2 толщиной V4 для исключения отражения от нижней стороны подложки.
В случае одинаковых показателей преломления подложки и резиста энергия поглощенного в единицу времени (интенсивность) света / и концентрация абсорбентов т связаны соотношением:
|
|
(1.22)
где х— расстояние от поверхности резиста; т,- — молирная концентрация (-го компонента; а, — молярный коэффициент поглощения i-ro компонента.
Для позитивного резиста можно написать:
|
|
— I (х, t) [aimi (х, t) + а2пгг (х, t) + аътъ (х, /)] (I. 23)
где t — время экспонирования.
Изменение концентрации ингибитора экспонирования определяется выражением:
|
drrii (х, t) It |
|
(1.24) |
= — Ш (х, t) I (х, t) С
где С — отношение скорости распада ингибитора к интенсивности света.
При введении начальных условий: I (0, t) = /0, т1 (х, 0) = m°, т2 (х, t) = т°2, т3 (х, t)=m°l — ml (х, t) — получим соотношение (I. 25):
![]() - = - / (х, () (т, (х, 1) [а, - а3] + а2т“ + a3m5} (1.25)
- = - / (х, () (т, (х, 1) [а, - а3] + а2т“ + a3m5} (1.25)
После нормализации М {х, t) == щ(х, t)/m° получим выражение (1.26)
|
|
|
и (1.27) |
|
(1.26) |
I (х, t) [AM (х, t) + В]
|
(I. 27) |
|
|
|
Перед экспонированием М(х, 0) = 1, /(х, 0) = /0 ехр[—(А + В)х] и граничные условия на границе резист — воздух: /(ОД) = /0 и А1(0Д) = ехр[—/0(1)]. Полученные уравнения можно интегрировать численно для I(x, t) н M(x, t)t если известны А, В, С и 10. Пропускание пленки резнста Т дано соотношением |
|
[AM (x, t) + В] dx |
|
(I. 28)! |
|
t-i |
|
1 |
|
T (t) =* exp |
|
(I. 28) |
Уравнение (1.16) при 7"(0) сводится к (1.29):
Т (0) = ехр [— (Л + В) d] (1.29)
а при t-*- °° к (I. 30)
Т (оо) = exp (— Bd) (1.30)
Для скорости изменения пропускания справедливы уравнения (1.31) и
(1.32):
|
dt о |
|
dT(t) __TmJ М (х, t) dt б Так как согласно уравнению (1. 33) дМ (х, 0) |
|
dt |
|
dT (0 _ _ т {() J [АМ (Xi t) + в] dx (1.31) 0 = - Т (t) Л ^ - м (*’ dx (1.32) |
|
= - С/0 ехр [- (А + В) х] (I. 33) |
то начальное изменение пропускания определяется соотношениями (1.34) и (1.35);
TOC o "1-5" h z dT (0) d
|
dt dT (0) |
T (0) A ^ C/0 exp [- (A + B) x] dx (I. 34)
0
= T (0) [1 - T (0)] AI0C/(A + В) (I. 35)
dt
Таким образом, получаем систему асимптотических соотношений (1.36), (1.37) и (1.38) для А, В и С, включающих пропускание пленки резиста в начале экспонирования, начальную скорость изменения пропускания и пропускание полностью экспонированного слоя:
л =. (l/d) 1п [Г (оо)/г (0)1 (1.36)
В = — (1/d) In Т (оо) (1.37)
г — А+В rfH0) ,138>
Л/0Г(0) [1-7(0)] dt
При использовании монохроматического света и подходящего детектора можно измерять интенсивность света, проходящего через резист I и интенсивность /о. В качестве детектора можно использовать калиброванный люксометр и его данные в процессе экспонирования заносить в память ЭВМ. Обработка данных для Л, В и С проводится при помощи осуществляемой несколько раз
регрессии. Значения Л, В и С в полосах испускания ртутной лампы, а также
показатели преломления фоторезиста AZ-1350J приведены ниже (предварительный нагрев при 70 °С в течение 1 ч [1]):
|
К |
нм |
435,8 |
404,7 |
365,0 |
|
л, |
мкм-1 |
0,54 |
0,86 |
0,74 |
|
в, |
мкм-1 |
0,06 |
0,07 |
0,20 |
|
с, |
СМ2/Дж |
14 |
18 |
12 |
|
п |
1,65 |
1,70 |
1,72 |
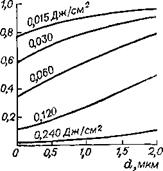
Определение значений Л, В и С дает возможность провести численное интегрирование полученных уравнений и установить распределение ингибитора в тонком слое резиста в зависимости от дозы излучения f0t вплоть до толщины 2 мкм по уравнениям (1.26) и (1.27) (рис. 1.27). Однако и при этой толщине распределение ингибитора в слое не является однородным, при экспонировании образуется концентрационный градиент ингибитора. Изменение скорости проявления резиста в зависимости от х дает возможность характеризовать процесс проявления прн определенном градиенте концентрации ингибитора.
Было создано специальное устройство, позволяющее непосредственно определять толщину слоя резиста в процессе проявления в зависимости от времени [83]. Измерение толщины основано на интерференционном принципе с использованием света с длиной волны 550—800 нм, в процессе опыта проводится 200—500 измерений.
|
|
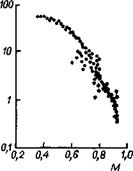
Найдено эмпирическое соотношение (1.39) между М и R, которое хорошо описывает опытные данные (рис. 1.28) в области высоких М; область ма-
|
|
Рис. 1.27. Зависимость доли непрореагировавшего ингибитора растворения М от толщины пленки фоторезиста d на неотражающей подложке при разных количествах экспонирующего света.
Рис. 1.28. Зависимость скорости проявления R резиста AZ-1350/в проявителе AZ : Н20 (1 : 1) при 20 °С (сушка при 70 °С) от доли непрореагировавшего ингибитора М.
лых М трудна для аналитической проработки, поскольку значения R в ней очень большие:
R = exp (Ei + Е2М + Е3М2) (I. 39)
где Е! — Еъ экспериментально определяемые коэффициенты.
Автоматизация всех аналитических определений весьма упрощает нахождение R.
Эту простую модель можно распространить и на системы, где имеет место отражение от подложки и границы резнст — воздух, т. е. интерференционный эффект, и таким образом получить характеристики профиля рельефа. Ее использование в проекционном экспонировании [35] требует учитывать в расчетах неоднородность интенсивности света в слое резиста и соответствующую ей неоднородность концентрации ингибитора.
С помощью соотношений, выведенных Берингом [86], найдена другая модель, описывающая рельеф края слоя резиста. Модель, разработанная Мак - Гиллисом и Ферсом [87], дает возможность оценить ширину линий; она учитывает дифракцию Френеля на краях маски. Уход размеров линий Д в резисте, отвечающих прозрачным участкам маски, определяется соотношением (1.40):
Д = as0-5 In Е( — In Ej, + 1п К (I. 40)
где а и К — константы, характеристические для используемой экспозиционной системы; s — расстояние между маской и подложкой; Et — энергия падающего излучения; Ет — энергия начала экспозиционного процесса.
Модель показала существование оптимального экспозиционного отношения EijEr, при котором достигается минимальная разница в ширине линий для всех
методов экспонирования.
Модель экспонирования негативного фоторезиста и математическую обработку процесса структурирования в зависимости от распределения молекулярной массы фотополимера предложили Райзер и Питтс [88].

 Опубликовано в
Опубликовано в