Задача оптимизации сводится к определению экс­тремума (максимума или минимума) целевой функции. Эта проб­лема возникает всякий раз, когда необходимо решить задачу преимущественного улучшения двух или более количественных характеристик, различным образом влияющих на процесс [33, 86].

При сопоставлении матриц планирования линейного двух­уровневого эксперимента и матрицы центрального композицион­ного ротатабельного планирования второго порядка обнаружи­вается существенное различие в объеме эксперимента. Ставя задачу оптимизации целевой функции, целесообразно использовать при движении к области существования экстремума двухуровне­вое планирование.

Методы оптимизации, используемые при обработке опытных данных, широко применяются в задачах оптимального проекти­рования аппаратов и систем. В задачах движения к области экс­тремума при оптимизации эксперимента оправдано лишь приме­нение градиентных методов, использующих уравнение регрессии (функции цели), которое базируется на двухуровневом экспе­рименте.

При исследовании диффузных систем, как правило, доста­точно установить область существования экстремума функции цели.

Изложенные методы планирования двухуровневого экспери­мента, приводящие к линейным моделям функции цели, позво­ляют использовать градиентные методы движения в области экстремума.

В общем случае градиент целевой функции имеет вид

&‘*ут = $!г11+т11+ +1г/' <|5-18>

Где — частные производные по независимым факторам X,-; I— 0/ £

Единичные векторы в направлении координатных осей.

Эффективность градиентных методов существенно зависит от характера изучаемой поверхности отклика (функции цели), выбранного шага движения к оптимуму, значения ошибок эксперимента и других факторов. Техника поиска экстремума
основана на расчетах, которые позволяют определить направ­ление наиболее быстрого оптимизируемого критерия.

Основной вопрос, решаемый в методах градиента,— опреде­ление направления градиентного вектора и выбор шага движе­ния по градиенту: выбор значения шага в направлении grad У в значительной мере обусловлен видом поверхности отклика (функции цели). Если шаг слишком мал, потребуются продол­жительные расчеты. Если он слишком велик, можно миновать оптимальное значение. В некоторых градиентных методах шаг изменяется в процессе движения к оптимальному значению, так как это повышает эффективность поиска экстремума.

Остановимся на методе крутого восхождения (наискорейше­го спуска). Пусть с помощью полного или дробнофакторного эксперимента получена линейная модель объекта исследования

К

(15.19)

Y = Ьо + Ц biXi.

Знание линейной модели позволяет находить область опти­мальных значений путем движения по градиенту. Коэффициент регрессии каждого фактора равен по значению и знаку соответ­ствующей частной производной функции цели.

При выборе шага движения по градиенту за основу выби­раем шаг наиболее существенного фактора. Если значения кри­терия оптимизации далеки от оптимального, то выбираем шаг основного фактора, обеспечивающий быстрый выход за пределы области проведенного эксперимента.

Обозначим интервал варьирования е, шаг фактора И и коэф­фициент регрессии Ь основного фактора индексом р. Тогда шаги по всем остальным факторам

(15.20)

Выполнив мысленные (расчетные) опыты, определим значе­ние функции цели. После каждого рабочего шага оценивается приращение ДУ. Если оно оказывается положительным, движе­ние происходит в правильном направлении и следует двигаться дальше. Если же результат измерения показывает, что ЛУ<0, то рабочее движение прекращается и начинается новая серия пробных движений. При этом определяется grad У в новой точке и продолжается движеиие по новому найденному направлению. Полученные расчетным путем параметры оптимизации требуют проверки экспериментом.

Пример. Используя методы планировиния эксперимента, находим оптималь­ное конструктивное решение деаэрационной колонки струйного типа.

Ставя задачу об оптимальном конструктивном решении, как и в любой за­даче планирования необходимо выбрать параметры состояния (функцию цели) и факторы, которые войдут в план эксперимента.

В деаэрационных колонках деаэрация осуществляется обычно в двух сту­пенях — струйной и барботажной. Чтобы процесс деаэрирования в барботаж - ной ступени был эффективен, недогрев воды до температуры насыщения перед - барботажной ступенью не должен превышать 4—5°С. Вместе с тем деаэратор — это и подогреватель питательной воды котельной установки. Поэтому одно­значное определение функции цели, относительно которой будет осуществлять­ся оптимизация проектного решения, затруднено. Следуя теории планирования эксперимента, выделяем два переменных состояния: недогрев воды до темпера­туры насыщения и сстатсчрю кскиеьтрагно ккслсрода в Еоде. Пссле расчет ного исследования каждой из них решим компромиссную задачу.

Геометрия колонки определяется рядом параметров, которые обычно эа,- даются как конструктивные. Поэтому вопрос оптимального их выбора пред­ставляет интерес для разработки подходов в проектировании, обеспечиваю­щих внедрение в инженерную теплоэнергетическую практику методов автома­тического проектирования.

Для анализа работы деаэраторов следует выделить те геометрические фак­торы, которые наиболее существенно влияют на процессы подогрева воды и де­сорбции. Необходимо вместе с тем выбирать только те факторы, внутренние связи между которыми минимальны. Одновременно это должны быть факторы определяющие общие геометрические размеры конструкции.

Естественно, оптимизация конструктивного решения должна осуществляться для заданной производительности аппарата.

Приняв скорость выпара на выходе из горловины питающей тарелки не более 0,2 м/с, чтобы исключить возможность уноса воды, при заданном коли­честве выпара из уравнения неразрывности течения найдем диаметр горлови­ны Ог.

Так как диаметр а!0 и длина Ь струй определяют процессы подогрева и де­сорбции воды, они однозначно входят в число определяющих факторов.

Скорость воды в струях зависит главным образом от гидростатического уровня воды Лг с Уровень воды на тарелке не принадлежит к геометрическим характеристикам, однако он определяет высоту борта на тарелке Яб, и поэтому в задачах оптимального проектирования может приниматься в качестве фактора.

Экспериментально установлено, что взаимодействие парового потока и струй жидкости наиболее эффективно при шахматном расположении струй на равно­стороннем треугольнике. Диаметр и шаг струй при заданных производитель­ности и Лг с определяют количество отверстий на тарелке и живых сечений для потока пара, поэтому шаг отверстий 5 принимают в качестве определя­ющего фактора. Все остальные геометрические параметры, прежде всего диаметр и высота колонки, оказываются производными величинами.

Таким образом, п число определяющих факторов необходимо включить ве­личины с1а, 5, Лг с.

Поскольку методы планирования позволяют организовать решение задачи при минимальном сбъсме расчетного эксперимента, то при четырех факторах наиболее целесообразно 'использовать матрицу планирования дребно-фактор - ного эксперимента— полуреплику 21-1. При этом реплика строится на основе матрицы трехфакторного эксперимента, когда четвертый фактор генерируется тройным взаимодействием Х|, Х.2, Х3.

Матрица планирования в этом случае принимает вид табл. 15.12.

Опыт проектирования указывает, что геометрические факторы, выбранные в качестве определяющих, изменяются в таких пределах: й0 = 5ч-8 мм;

5 = 18 20 мм; /, = 3004-500 мм; /1ГС=50-н80 мм.

С учетом этих данных точку центра плана, интервалы варьирования фак* торов и их кодированные значения представим в табл. 15.13.

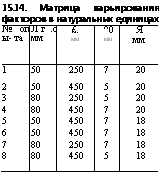
В соответствии с матрицей планирования представим уровни факторов для проведения расчетного эксперимента в физических переменных в табл. 15.14.

Для решения оптимизационной задачи требуется выполнение вариантных расчетов при комбинации геометрических факторов в соответствии с условиями

15.13. Уровни варьирования факторов в натуральной ко­дированной форме Фактор Натуральные значения Кодированные значения Верхний ОСНОВНОЙ Нижний Верхним ОСНОВНОЙ Нижний *1 №г. е> 80 65 50 + 1 0 —1 *2 (Ц 450 350 250 + 1 0 —1 *3 <<У 7 6 5 + 1 0 —1 *4 (Я) 20 19 18 + 1 0 —1

15.14. Матрица варьирова­ния факторов в натуральных единицах № оп ы - та Л г. с мм £. Мм ^0 Мм Я Мм 1 50 250 7 20 2 50 450 5 20 3 80 250 5 20 4 80 450 7 20 5 50 450 7 18 6 50 450 7 18 7 80 250 7 18 8 80 450 5 18

15.12. Матрица планирования дробно­факторного эксперимента 2К—1 (полу - репликз) *0 (»ГС» *1 <*-> Х2 И о) *3 *4<*?*2*3> +1 —1 — 1 + 1 + 1 +1 —1 + 1 — 1 + 1 ^2 +1 +1 — 1 — I + 1 *3 +1 +1 + 1 + 1 + 1 У А +1 —1 — I — 1 — 1 *5 +1 —1 + 1 + 1 — 1 +1 — 1 + 1 — 1 *7 +1 +1 + 1 — 1 — 1

опытов № 1—8. В целях оперативности следует применять машинные методы теплового и десорбцнонного расчетов деаэрационной колонки.

Программы этих расчетов на ЭВМ типа «Наири-К» и сводные таблицы физических и машинных переменных к программам приведены ниже.

Ограниченность оперативной памяти машин инженерных расчетов типа «На - ири» и «Мир» обусловливает расчленение задачи оптимизации конструктивных факторов по параметру состояния (функции цели) на ряд отдельных программ: тепловой и десорбциоиный расчеты вариантов, определение уравнения функции цели и движения к области экстремума при двухуровневом расчетном экспе­рименте.

Программы определения уравнения функции цели, таблица физических и машинных переменных, а также программа решения задач движения к об­ласти экстремума градиентным методом для ЭВМ «Наири-К» приведены далее.

15.15. Физические и машинные переменные к программе теплового расчета струйной деаэрационной колонки

Физические перемен­ные	Переменные на языке АП	Физические перемен­ные	Переменные на языке АП
О* Ин. п	Аі	Число некипящих потоков +1	Й
Ог. п	Ь1	Число кипящих потоков +1	Ж
	Сі		Г1
1к. п	“і	И	Г2
■г	Тік	('п	Г3
Тк П. ср	Шіп	Глв	Г4
СД. В	Щ	Рп	Г5
Чк	Чк	А	Гб
*о,	Д/	Количество таре­лок (секций)	Г7
Ч	5І	О,	Г9
К.„	Чк	‘ср	Г1С
Л'о	°к	О,	Г11
0Г			Г12
Гд	Ф	^вып	Г13
<?п. к	Хк
Количество опытов	Ь	Оп	Г14
**		О;	Г15
'■к	Гк	Е2	Г1б
Ов. К	К	Количество рядов отверстий на та - Релке	Ык

К программе десорбционного расчета струйной деазраиионной

Колонки

Физические пере­менные	Переменные на языке АП	Физические пере* менные	Переменные на языке АП
Р6,	Г,	Ро2	Ц
Р'п К	Рм	Р0. о	Ф
Аа	Ам	Коэффициент В	Ж
Рв	“/*	А1	О,
С0г (насыщения)	С! к		Н
С0 (расчет)	Ч1к	Рв 1
Li*	Л/*	*1	Ух
Do 1	Д/	*/*	Ьк
Wok	ТМ |	Количество отсе­ков + 1	Й
®п. к	Ш/* 1	Количество опытов	Ь
О;, к	*/*	Количество ступе­ней поперечно-точ­ных
Оп. к	11к ||

Программа теплового расчета деаэрациониой колонки

I =. Ю к = 10 л I т. и ( = 20 ^ * 1

Г = 5 о с Ь и & = 10 < е г ж ы о

1. Введем ф Ц ш й ж ь

2. Допустим 1 = 0 6=0

3. Введем и( с(.

4. Вставим ( = I + I 6=6+1

5. Вычислим з = II — б

6. Если з > 0 идти к 3

7. Допустим ( == 0 6 = 0

8. Введем Ь1 и,

9. Вставим / = < + 1 6=6 + 1

10. Вычислим ж — б

11. Ьсли < > 0 идти к Я

12. Допустим / = 0 4 = 0 ’■ = I

13. И ведем д( в, л1)г 1/к Г,

14. Вставим / = / + 1 К = к + 1 6 = = 6 + 1 I [ + 1

15. Вычислим з = ь — 6

16. Если з > 0 идти к 13

17. Допустим 1 = 0 6 = 0 н=0

18. Вычислим н = и + а(с1

19. Вставим (=(+! 6=6+1

20. Вычислим з = й — б

21. Если з > 0 идти к 1й

22. Допустим I = С 6 = 0 м == 0

23. Вычислим м = м + Ь1и1

24. Вставим ( = ! + 1 б = 6+ 1

25. Вычислим э = ж — б

26. Если я > 0 идти к 23

27. Вычислим г15 = (щ • г4 + г,3 X г, - н - м)/(г, - г4)

28. Допустим =0 б=0н = 0м = 0

29. Вычислим и = (и + Ь( (и-—г4)/ф)Х X г1 м = м + Ь( (и(- — г4)/ф

30. Вставим £ = £ + I 6 = 6+1

31. Вычислим з = ж — б

32. Если с > 0 идти к 29

33. Вычислим г10= (г15-г3+н)/(г15+ + м)

34. Допустим ( = 0 6 = 0 н = 0

35. Вычислим и = н + а( (г4 — с()

ЗС. Вставим { = I + 1 6=6+1

37. Вычислим з = й — 6

38. Если з > 0 идти к 35

39. Вычислим г14= н/(г10 — г4)

40. Печатаем с 2 знаками г10 г14 г15

41. Допустим / = 0 р = О

42. Допустим к = О

43. Допустим ( = 0 6=0 н = 0 м = 0

44. Вычислим н = и + а1-сс м = м + а1

45. Вставим 1 = 1+1 6=6+1

46. Вычислим з = й — б

47. Если з > 0 идти к 44

48. Вычислим гк = и/м = г^/4,186 ей = м

49. Вычислим т.[к = 0,675ехр (0,5 1пх X (19,62 • 11к)) о» = 4е6/я^/им

50. Печатаем с 3 знаками гк (к гк

51. Допустим п=0н = 0ч = 0 6=1

52. Вычислим н = (н + *,/5) ч = ч+ +

53. Вставим я = я + 1 6 = 6+1

54. Вычислим у = ок — ч

55. Если у > 0 идти к 52

56. Вычислим б = б — I

57. Допустим ыА = б

58. Вычислим г9 = У"5) гп = ■=* (ц +

Г12 = ’'л/*Гц(1 —Д/Л/)

Г16 = о — Я//51;)

59. Допустим м = 1

60. Вычислим н =

61. Вычислим м = м + 1 и = » +

+ 5 3 = ы* — м

62. Если з > 0 идти к 61

63. Вычислим ок = (-ы^ц+ н)^

64. Печатаем с 2 знаками окык

65. Допустим и = 0 Шул= 1

66. Вычислим ч=ехр (0,31п н=ехр (0,7 1п Ду) м=ехр ((г0Л/й,'х Хч/н) 1п 10) (/= г2 — (г2_^/м

67. Вычислим м = Од, ч=е^ (4,186г/______

• —2*)/( Г3 —4,186(/) н = ей + ч

68. Вставим к = к -|- I

69. Допустим хк = ч ^ ^ е* = н

Ок = ы

70. Вычислим г*=4,186^ г,3=01002щ

71. Допустим н = г13 з=6

72. Допустим А = I 6=1

73. Вычислим н = н + *4 ч = н —

— хк м = з — 6

74. Если м < 0 идти к 77

75. Вставим & = 6 + 1 6 = 6+1

76. Идти к 73

77. Вычислим #=н/г5 • г,2 м=ч/г5х X г16 6= ^/м

78. Если б> 1,25 идти к 81

79. Вычислим ч = (у + м)/2

80. Идти к 82

81. Вычислим ч — (у — м)/2,3 ^ (у/м

82. Вычислим з = ч —

83. Если з > 0,1 идти к 85

84. Идти-к 88

85. Вставим л = л + 1 к — к — 1

86. Допустим ш/п = ч

87. Идти к 65

88. Вставим п = я + 1

89. Допустим = ч

90. Печатаем с 3 знаками хк ^ ш/л °к

91. Вычислим (/*= (4ел/т1Д^ . х X 0,675)2/19,62

= 0,675 • ехр (0,5 1п (19,62 X X ',*))

92. Допустим 6 = к

93. Вычислим з = б — г7

94. Если з < 0 идти к 51

95. Вычислим ч = ехр (0,5 1п (л(7г/д;)) и = 1/ехр (0,3 1п т1к)

М = ехр (0,0586 • ч ■ н • 1п 10) г/= = г2-(г2-^)/м

96. Вычислим ч=е(г(4,186{/——

— 4,186 у) н = е^ + ч

97. Вставим £ = к1

98. Допустим хК = ч = у ек = н

99. Вычислим гк — 4,186/^

100. Печатаем с 2 знаками хк (к ек гк

101. Вставим /=/+1 р = р + 1

102. Вычислим з = ь — р

103. Если з > 0 идти к 42

104. Кончаем Исполним 1

( = 12 о I ы х / = 10 д г Ь

1.

Программа десорбционного расчета струйнойдеаэрационной колонки I = Ю И = 4 л т ш е х < а о и с ч 33. Вычислим з = и — б

Введем ц ж ф ь и

2. Допустим ( = 0

3. Введем оI 1( ы,- х1

4. Вставим /=[-(- 1

5. Если (' — 11 <0 идти к 3

6. Допустим — 0 ц = 0

7. Допустим к = 0 6=0

8. Введем л,* т;> ш/)г е/)г /;(г

9. Вставим £ = й + I 6 = 6+1 Ю. Вычислим з = и— б

11. Если з > 0 идти к 8

12. Вставим /=/-(-1 ц=ц+1

13. Вычислим з = ь — ц

14. Если я > 0 идти к 7

15. Допустим / = 0 6 = 0

16. Введем Д/ Гу 6;-

17. Вставим / = / + 1 6=6+1

18. Вычислим з = и — б

19. Если з > 0 идти к 16

20. Допустим / = 0 ш = О

21. Допустим 6=0 6 = 0

22. Допустим м = (

23. TOC o "1-5" h z Программа и п (0 1 1 у м г)

24. Вычислим вд = г

25. Допустим м =

26. Программа и п (I 1 1 у м г)

27. Вычислим р-к — г

28. Допустим м = 1^

29. Программа и п (ы 1 1 у м г)

30. Вычислим Ыд = г с/4=21 • Ю^а^Х

31. Печатаем с 3 знаками

32. Вставим А = £ + 1 6=6+1

34. Если з > 0 идти к 22

35. Допустим к = 0 6 = 0

36. Вычислим Ь2 =

37. Вычислим з=ехр (0,5 1п е(-й)/ехрх X (0,3 1п т^) ехр (0,7 1п д;)

38. Вставим £ = £ + 1 6=6+1

39. Вычислим н=ехр(0,3 [пш^/ехрх Х(0,51п^

.9=6г/ехр (жл/д, 3 • н 1п 10)

40. Вычислим з = ($/£,-*) — 1

41. Если з > 0 идти к 47

42. Допустим Ч]к = % Ь2 = э

43. Печатаем с 3 знаками ч(4

44. Вычислим з = Ьй — 6

45. Если з > 0 идти к 37

46. Идти к 52

47. Допустим ч/к = с(к ь.2 =

48. Печатаем с 3 знаками ч^

49. Вычислим з = Ь0 — 6 £0. Если з < 0 идти к 37

51. Идти к 52

52. Вычислим н = ехр^.о^л^/с^Х Х/ехр (0,3 1пт/й)

.ч = Ьр/ехр (0,0211 • н 1п 10)

53. Вставим £ = £ + 1 6=6+1

54. Допустим ч^ = 5

55. Печатаем с 3 знаками ч/к

56. Вставим / = ( + 1 ш = ш + 1

57. Вычислим з = ь — ш

58. Если з > 0 идти к 21

59. Кончаем Исполним

15.17. Физические и машинные переменные к программе определения уравнения функции цели и движения к области экстремума Физические нерешен­ные Переменны* на языке АП Физические перемет­ные Ромениыг на языке АП У, Координата центра плана И1 'V. с, Л1/ ы **. И2 Ч (ХЦ) *30 И* “о, *3! * ^11) 1 а*

5,	Чі (хц)	Фиктивный фактор X,	О 1) *
Интервал варьиро­вания Нг	--------------------- «і		Л
	Є« 1 ^пых
4,	«5	Количество опытов	Й
5		Количество факто - ро»
Шаг факторов пг	Щ,	Количество расчет­ных циклов (групп опытов)	Р
І	Шг	Условно допусти­мое количество циклов	Ь
	Ш,
5	Ш4	1 ]г

Программа определ^ия УР*«»ни функции цели и дви­жения к области э«стРемУма 8 заДаче выбоРа оптималь­ных геометрических характеристик отсека деаэрационной колонки

/= 10 Ь е ш и I I /=10 £=32х £=32у

1. Введем й ф л г р ь

2. Допустим £=1 6=1

3. Введем у(

4. Вставим £=£+1 6 = 6 + 1

5. Вычислим з = й —б

6. Если з>0 идти к 3

7. Допустим / = 0, М = О

8. Допустим £= 1 6=1

9. Введем X/1

10. Вставим 1=£+1 6 = 6+1

11. Вычислим з=й —6

12. Если з>0 идти к 9

13. Вставим /=/+1 м = м +1

14. Вычислим з=ф — м

15. Если э»0 идти к 8

16. Допустим /=1 м = 1

17. Введем е/ Ш/ г//

18. Вставим /

19. Вычислим

20. Если з»0

21. Допустим

22. Допустим

23. Вычислим

24. Вставим £

25. Вычислим

26. Если з»0

27. Вычислим

28. Печатаем

29. Вставим /

30. Вычислим

31. Если з»0

32. Допустим

33. Вставим /

34. Вычислим

=/+1 м=м+1 з = ф — м идти к 17 /=0 м=0 £=16=1 н=0 н = н + хц-у( =/+1 6=6+1 3 = й — 6

Идти к 23 Ь/ = н/й с 4 знаками Ь/ =/ +1 м = м + 1

З = ф — м идти к 22 /=0 н = Ь/ 6 = 0 =6+1 6=6+1 н=н — Ь/и/І Ш/

35. Вычислим э = ф — б

36. Если з > 0 идти к 33

37. Допустим / = 0 / j = н 6 = 0

38. Печатаем с 4 знаками £у

39. Вставим / = / - f - 1 6 = 6+1

40. Вычислим tj=bj/uij

41. Вычислим э = ф—б

42. TOC o "1-5" h z Если э > 0 идти к 38

43. Допустим / = 1 с = | bj | м = 1

44. Допустим / = | bj | ж = /

45. Если м > й идти к 52

46. Вставим / = / + 1 м - м + 1

47. Допустим а = | £>у1

48. Если о > б идти к 44

49. Если а > с идти к 46

50. Допустим с = а

51. Идти к 45

52. Печатаем с 3 знаками б ж

53. Допустим j = ж

54. Вычислим а - Шу/6уе( /у = а

55. Вычислим м = ж — 1

56. Если м > 0 идти к 59

57. Вычислим < = ж + 1

58. Если н < ф идти к 68

59. Идти к 66

60. Допустим / = м м = м — 1

61. Вычислим /у = а&уву

62. Идти к 56

63. Допустим / =■ и н = н -)- I

64. Вычислим /у = abjtj

65. Идти к 58

66. Вычислим т = рй ш.=(р—1)й+1

67. Допустим i = щ д = щ ц=1

68. Допустим / = 1 6=1

69. Вычислим н = и у + ij • Ц

70. Допустим *,у=и

71. Вставим / = /+1 6 = 6 + 1

72. Вычислим з = й — б

73. Если з > 0 идти к 69

74. Допустим / = 0 м = <■ б = О

75. Вставим / = / + 1 6=6+1

76. Вычислил! м = м + ■

77. Вычислим з = ф — б

78. Если з > 0 идти к 75

79. Допустим у-1 = м

80. Печатаем с 2 знаками

81. Вставим г = 1 + 1 д = д _|_ 1 ц_ = Ц + 1

82. Вычислим з ■= т — д

83. Если з > 0 идти к 68

84. Допустим I = щ с = | у. | м = щ

85. Допустим б = |^| ж = £

86. Если м > т идти к 93

87. Вставим /' = £ + 1 м = м + 1

88. Допустим а = | у( |

89. Если а > 6 идти к 85

90. Если а > с идти к 87

91. Допустим с=а

92. Идти к 86

93. Печатаем с 3 знаками б ж

94. Допустим г = ж

95. Вычислим м = л — ус

96. Печатаем с 3 знаками м £

97. Если м < г идти к 103

98. Если р > 6 идти к 103

99. Вычислим р = р + 1

100. Вычислим щ = (р — 1) й + 1 т= = pH

101. Допустим £ = щ д = щ ц = щ

102. Идти к 68

103. Кончаем- Исполним 1