Температура неограниченного стержня, торец которого поддерживается при постоянной температуре описывается известным решением [4], рассмотренным в п. 1.1.5:

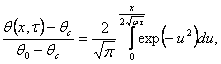(4.11)

Где – начальная температура стержня, – температура торца стержня.

При этом плотность теплового потока на торце стержня равна:

(4.12)

А количество теплоты, поступившее за время T, будет [1]:

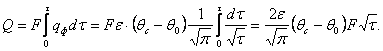(4.13)

Для стержня, на торце которого непрерывно действует источник тепла постоянной плотности , справедливо решение вида (4.1) с той лишь разницей, что температура заменена плотностью теплового потока [4]:

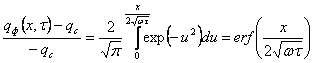. (4.14)

Распределение температуры в стержне найдется интегрированием (4.14) [4]:

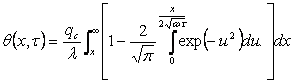. (4.15)

При этом в плоскости контакта (т. е. при X=0) зависимость температуры от времени описывается функцией [1]:

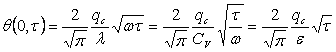. (4.16)

Где

Температуру торца стержня после прекращения действия источника в момент времени можно определить путем суперпозиции, т. е. наложения двух решений для температуры от источника тепла Q, действующего в интервале времени и равного ему по величине, но противоположного по знаку стока , действующего в интервале времени (рис. 4.16).

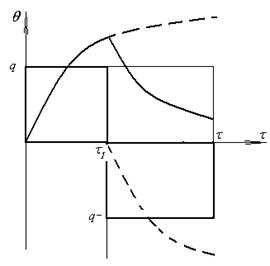
Рис. 4.16. Схема к определению контактной температуры после прекращения действия источника

Источник тепла продлим до времени , а с момента времени включим равный ему по мощности сток. Результирующая температура от источника и стока определится по формулам [1]:

(4.17)

Рассмотрим Задачу о распределении температуры в бесконечном стержне от движущегося вдоль стержня непрерывно действующего точечного источника тепла постоянной мощности.

Задачи расчета температурного поля от движущихся источников рассматривались Н. Н. Рыкалиным [8], Дж. К. Иегером. Для того, чтобы учесть движение, период действия источника разбивают на малые интервалы и в каждом из таких интервалов определяют приращение температуры от точечного мгновенного источника тепла. Если постоянный точечный источник тепла движется со скоростью V, то его положение в момент времени T¢ после начала нагрева определится координатой X = V T¢ (рис. 4.17).

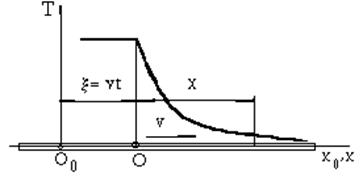
Рис. 4.17. Схема замены постоянного точечного движущегося источника тепла мгновенными

Для мгновенного точечного источника тепла, выделившего тепло в точке О (рис. 4.15), время T² выравнивания тепла равно T² = T-T¢. Подставив значения координаты X0 и времени T² в функцию точечного источника (4.7), получим [8]

. (4.18)

Температура за время действия источника от 0 до T [8]

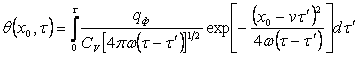. (4.19)

Практический интерес представляют приращения температуры при установившемся температурном режиме, т. е. при T ® ¥ и, соответственно, при T² = T-T¢ ® ¥. При этом зависимость температуры от координаты X (4.19) существенно упрощается и приводится к виду [8]:

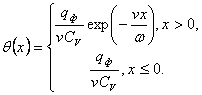(4.20)

Здесь – плотность теплового потока, равная , в .

Таким образом, за движущимся источником тепла температура постоянна, в то время как перед ним температура убывает по экспоненциальному закону, причем тем быстрее, чем выше скорость V (рис. 4.18).

Полученное решение (4.20) качественно характеризует распределение температуры в средней части сварного шва. В частности, при дуговой электросварке с постоянной мощностью чрезмерное увеличение скорости перемещения электрода вдоль шва приведет к уменьшению температуры. Следствием этого может быть недостаточное заполнением шва расплавленным металлом, снижение качества сварного шва. Уменьшение скорости перемещения дуги приведет не только к снижению производительности сварки, но и к перегреву расплавленного металла и также ухудшит качество сварного шва. Таким образом, выбор мощности сварки и скорости перемещения электрода должны быть согласованы.

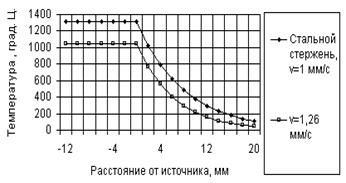
Рис. 4.18. Зависимости температуры стержня от расстояния от движущегося источника тепла с плотностью теплового потока