Свободные незатухающие колебания в системах с двумя степенями свободы. Нормальные колебания (моды). Парциальные и нормальные частоты. биения. Понятие спектра колебании. Методика анализа колебании двух связанных осцилляторов. Зату­хание колебании и диссипация энергии. .Вынужденные колебания. Резонанс. колебания систем со многими степенями свободы. Дисперсионное соотношение.

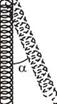
Наблюдая колебания массы т, подвешенной на легкой пружине жесткости kx, нельзя не обратить внимание на то, что, наряду с вертикальными колебаниями груза, возникают и так называемые маятниковые колебания (из стороны в сторону) — см. рис. 3.1.

Наиболее сильными эти маятниковые колебания будут тог-

да, когда частота вертикальных колебаний д/kj / m будет равна удво­

енной частоте маятниковых колебаний yfgTa (а — длина растяну - k

/ S Г 1 /

той пружины при неподвижном грузе). Такой результат легко понять, если рассматривать маятниковые колебания как резонансные пара­метрические колебания, при этом параметр маятника — длина пру­жины а — меняется при вертикальных колебаниях на величину +Да

(см. предыдущую лекцию). В течение некоторого времени маятнико-

m Рис. 3.1.

вые колебания могут усиливаться за счет уменьшения энергии верти­кальных колебаний. Затем процесс пойдет в обратном направлении:

маятниковые колебания начнут ослабевать, «возвращая» энергию уси­ливающимся вертикальным колебаниям. Следовательно, вертикальные колебания не будут гармоническими, что связано с наличием маятниковых колебаний, соответствующих воз­буждению второй степени свободы. При определенных условиях могут возникать и кру­тильные колебания груза вокруг вертикальной оси пружины. Опыт показывает, что наиболее сильными эти колебания будут в том случае, когда их частота, Jk2 / J (&2 — коэффициент жесткости пружины при ее скручивании, рассмотренный в лекции по деформации твердого тела, J — момент инерции тела относительно вертикальной оси) будет примерно в два раза меньше частоты вертикальных колебаний. В общем случае в этой системе могут происхо­дить четыре типа колебаний, соответствующих четырем степеням свободы: одно вертикаль­ное, два маятниковых в двух взаимно-перпендикулярных плоскостях и одно крутильное.

Таким образом, перед нами возникает задача изучения основных закономер­ностей колебаний в системах с двумя, тремя и более степенями свободы, затем можно рассмотреть и колебания сплошной среды, как системы с бесконечно большим числом степеней свободы.

Свободные незатухающие колебания в системах с двумя степенями свободы.

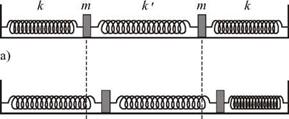
На рис. 3.2 изображены три различные колебательные системы с двумя степенями свободы. Первая из них (а) — это два различных пружинных маятника, связанные пружиной с жестко-

//////

//////

1i

к'

J m 2

Q 0

0

В)

m1 к1	к2 m
тшшшшїС smmmm
—1-------------- ►	—1-------------- ►
0 s 1	0 s2
s1	s2
a 1 a	2 a
, m,	m 2

а)

б)

Рис. 3.2.

стью к'. Вторая (б) — два груза с массами и Ш2, закрепленные на натянутом некоторой силой F невесомом резиновом шнуре. Третья (в) — два связанных пружиной к' различных маятника, каждый из которых состоит из груза, подвешенного на невесомом стержне.

Колебания грузов в каждой из трех систем описываются двумя временными зависимостями их смещений s 1 (t) и ^(t). Положительное направление смещения s на рисунке указано стрелками.

Опыт показывает, что при произвольном способе возбуждения колебания не будут гармоническими: амплитуда колебаний каждой из масс будет периодически меняться во времени. Однако можно создать такие начальные условия, при которых каждый груз будет совершать гармонические колебания с одной и той же частотой w:

(3.1)

s1 (t) = s01 sin(wt + j); s2(t) = S02 sin(wt + j).

Частота этих колебаний w определяется свойствами системы. Отношение

(3.2)

V = s02/s01

также определяется параметрами системы. Эта безразмерная алгебраическая величина V называется коэффициентом распределения амплитуд при гармоническом колебании. Отметим, что S01 и S02 могут иметь любой знак. Если V >0, то смещения обеих масс всегда происходят в одну сторону (синфазные колебания), а при V <0 — в противоположные стороны (противофазные колебания). Гармонические колебания (3.1) называются нормаль­ными колебаниями, или модами, а частота w называется нормальной частотой. Таким об­разом, мода характеризуется двумя параметрами: частотой w и коэффициентом V, опреде­ляющим «конфигурацию» моды.

Практика показывает, что в системе с двумя степенями свободы могут суще­ствовать синфазные гармонические колебания с частотой wI и противофазные гармони­ческие колебания с частотой wn > WI.

Следовательно, в системе могут быть возбуждены две моды:

s/(t) = s01sin(wIt + jj);

I мода s2(t) = S()2 sin(wit + ji);

s“(t) = SMsin^ + jII); II мода s2I(t) = s0I2sin(wIIt + j II); VII = s02 / Soi < 0.

(3.4)

Нетрудно теперь понять, что любое колебание связанной линейной системы с двумя степенями свободы (а именно такие системы мы будем далее рассматривать) мо­жет быть представлено в виде суперпозиции двух нормальных колебаний (3.3) и (3.4): si(t) = si (t) + s“(t) = s0! sin(wit + ji) + s01 sin(wnt + jii); (3 5) s 2 (t) = s 2 (t) + s 21 (t) = s02 sin(Wit + j i) + s02 sin(wnt + j ii). Не прибегая пока к детальному математическому исследованию, проанализи­руем поведение системы с двумя степенями свободы, пользуясь основными идеями, развитыми в предыдущих лекциях. Представим любую из систем, изображенных на рис. 3.2, как сложную систему, состоящую из двух парциаль­ных систем. Эти парциальные системы, соответ­ствующие случаю (а) рис. 3.2, показаны на рис. 3.3: каждая из этих парциальных систем имеет собственную частоту колебаний, которая называется парциальной частотой.

ki

k'

m,

k'

m2 чи

Рис. 3.3. Величины этих парциальных частот, соответственно, равны:

к, + к' ;

^2 + к

(3.6)

Ю, =

Ю2 =

Совершенно очевидно, что частота Ю, — это частота колебаний массы m, в системе двух связанных маятников, когда масса m2 неподвижна (заблокирована вторая степень свободы). Аналогично, с частотой Ю2 будет колебаться масса m2 , когда неподвижна масса m,.

-►

St

-►

So

б)

Теперь перейдем к определению нормальных частот wI и wII. Вспомним, что квадрат частоты гармонических колебаний равен отношению воз­вращающей силы к смещению гру­за s и величине его массы m. Под­берем начальные смещения масс mi и m2 таким образом, чтобы для обеих масс эти отношения (а, сле­довательно, и частоты) были бы одинаковы. Такой подбор легко угадывается для симметричной системы (m, = m2 = m, к, = к2 = к),

(рис. 3.4), у которой парциальные частоты совпадают:

к + к'

(3.7)

Ю, = Ю2 =

Если оба груза сместить вправо на одинаковые расстояния s0, = s02 , то средняя пружина к' (пружина связи) не будет деформирована (позиция б). После отпускания пружина будет оставаться недеформированной. Поэтому каждый из грузов будет совер­шать гармонические колебания с одной и той же частотой

к

Wi =

(3.8)

которая и является первой нормальной частотой. Конфигурация этого синфазного коле­бания (моды) задается коэффициентом распределения амплитуд VI = +,.

наковые расстояния (позиция в), то пружина к' удли­нится на величину 2s02 . Поэтому к правой массе будет приложена возвращающая сила, равная - (ку02 + 2к's02), а на левую мас­су будет действовать в противо­положном направлении сила - (кї^, + 2к/s0). После отпуска­ния грузы будут совершать про­тивофазные гармонические ко­лебания со второй нормальной частотой

s II s02

(3.9)

Wii =

/к + 2к' m '

Конфигурация второй моды характеризуется коэффициентом распределе­ния Vii = - L

Если грузы, изображенные на рис. 3.5а, сместить на произвольные расстояния (например, в одну сторону на величины s0, и s02, как это изображено на рис. 3.5б), то это эквивалентно суперпозиции двух типов начальных смещений: в одну сторону на оди­наковые величины (позиция в)

(3Л0)

s0, = s02 = (s0, + s02) ;

и в разные стороны (позиция г) на величины

- s0I[ = s02 = 2(s02 - s0,) ■

(3.H)

Поскольку колебательная система линейна, то синфазные колебания, возникаю­щие после отпускания грузов в позиции (в), будут происходить независимо от присутствия

противофазных колебаний, возникающих при отпускании грузов в позиции (г). Смещения обоих грузов с течением времени будут описываться формулами (3.5), в которых амплиту­ды определяются равенствами (3.10) и (3.11), а начальные фазы jr = j п = p / 2.

Проанализируем более подробно колебания в системе, изображенной на рис. 3.5. Пусть мы сдвинули левую массу вправо на расстояние s01, а правую массу оставили в несмещенном положении (s02 = 0). После отпускания обоих грузов в системе возник­нут колебания. Из (3.10) и (3.11) определяем амплитуды мод: s01 = s02 = s01/2 ; - s01 = s02 = _s01 / 2 . Поскольку фазы jj = jn = p /2 (т. к. начальные скорости у грузов отсутствуют), то смещения

. . S01 ^01

s1 (t) = -^- cos Юг t + -^- cos wnt;

. . ^01 ^01 S2 (t) = -^- cos Wjt — cos Wjjt.

(3.12)

Производя суммирование тригонометрических функций в (3.12), получим:

ЮП - Юг ЮП + Юг

(3.13)

s1 (t) = s01 cos---------- 2----- 1 • cos------ 2------ 1;

. . . Wn - Юг Юп + Юг

s2(t) = s01 sin-------------------- 1--- • cos-------------- 1.

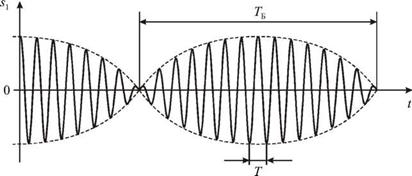
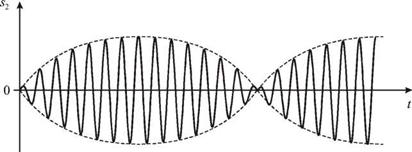
Временные зависимости (3.13) изображены на рис. 3.6.

Видно, что колебания каждой из масс имеют форму биений. Период этих бие-

1)

ний равен

где частота биений W б = Дю = юг1 - юг. Если ввести среднюю частоту Юг + юг1

юіі юі W 6

Тб =

Ю0 =

2p

то с этой частотой связан период колебаний Т =

2p

(3.14) (3.15) (3.16)

2р W0

Если частота биений Wб << Ю0 , как это изображено на рис. 3.6, то Тб >> T. В этом случае колебания обоих грузов будут почти гармоническими (квазигармонически - ми). Если переписать (3.13) с использованием средней частоты Ю0 и частоты биений W б в виде:

W б

(3.17)

sj (t) = s01 cos-^- t cos W0t = Aj (t)cos W0t; W б

s2 (t) = s01 sin t cos W0t = A2 (t) cos W0t;

Рис. 3.7.

то при Wб << w0 колебания (3.17) можно трактовать как колебания с частотой Ю0 и медленно меняющейся амплитудой A(t).

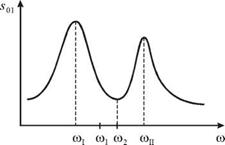
В теории колебаний и в других раз­делах физики для анализа колебательного процесса используют спектральное представ­ление, или спектр колебаний. Этот спектр изображают графически: по оси абсцисс ука­зывают частоты колебаний, а по оси ординат откладывают квадраты их амплитуд. Так, в частности, для колебаний, изображенных на

рис. 3.6 ( s1 или s2 ) и описываемых форму­лами (3.17), легко нарисовать спектр, по­скольку уже известно спектральное разложе-

ние этого колебания (представление в виде суммы гармонических колебаний), задавае­мое формулами (3.12).

Такой спектр изображен на рис. 3.7.

1) Колебания (3.12), вообще говоря, не являются периодическими, т. е. нельзя указать такое время T*, спустя которое они точно повторяются (отношение частот Юг / Юг1

- чаще всего ирпациональ - тю г = пю г1 будут исчезающе редки). Поэтому

ное число, а случаиих рационального отношения: ^

периодом биений Тб мы называем период (З. Т4) повторения огиоающеи суммарного колебания,

w г1

равный половине периода колебания с частотой іі

W б =

2р

= ^ - ют

, а

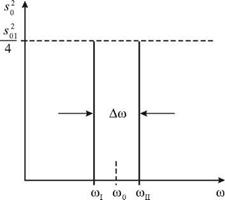
Этот спектр содержит две спектральные компоненты. Его можно охарактеризо­вать средней частотой ю0 и шириной Дю. В соответствии с формулой (3.14) произведе­ние Дю на период Тб равно постоянной величине:

Дю-Тб = 2я. (3.18)

Формула (3.18) имеет глубокое физическое содержание. Так, если происходит некоторое квазигармоническое колебание вида

s(t) = A(t)cos[w0t + ф(0], (3.19)

для которого амплитуда А и фаза j медленно меняются на масштабе времени t (рис. 3.8а), то спектр такого колебания может состоять из большого числа частот.

Эти частоты группируются вблизи центральной (основной) частоты ю0 = 2 я / T в пределах характерного интервала частот Дю, обратно пропорционального временно­му масштабу t. На рис. 3.8б изображен этот спектр, где по оси ординат отложен квадрат амплитуды s0 каждой из гар­монических составляющих, причем между t и Дю суще­ствует связь: Дю -1 ~ 2я.

s02(w)

w

Количественная связь между колебательным процес­сом s(t) и его спектром пред­ставляется (по аналогии с фор­мулами (3.12)) в виде суммы конечного или бесконечного числа гармонических состав­ляющих (в виде ряда или ин­теграла Фурье). Такое пред­ставление будет широко ис­пользоваться в курсе «Оптика».

Методика анализа колебаний связанных осцилляторов. Выше мы рас­смотрели колебания двух одинаковых связанных пружинных маятников, не прибегая к решению уравнений их движения. Однако, если жесткости пружин и массы тел имеют произвольные величины, то зачастую бывает трудно догадаться о конфигура­ции мод и их частотах. Поэтому представляется важным вооружиться универсаль­ным методом, позволяющим по единой схеме провести последовательный анализ любой колебательной системы с двумя степенями свободы, являющейся системой любых связанных осцилляторов.

Запишем уравнения движения двух связанных пружинных маятников в виде:

misi = - kisi - k 'si + k 's2; (3 20)

да2^2 = —k2 s2 — k '^'2 + k 'si.

Разделив первое уравнение на mi, а второе — на m2 и используя выражения (3.6) для парциальных частот, перепишем (3.20) следующим образом:

si = —Юі2 si — ais2,

2 (3.2i)

s 2 = a 2 si Ю2 s2 ,

где ai = —k' / mi, a2 = —k' / m2 — коэффициенты, зависящие от жесткости k' пружины свя­зи. Обратим внимание, что уравнения (3.2i) не могут решаться по отдельности, т. к. каждое из них содержит si и s2 . Поэтому целесообразно перейти от смещений si и s2 к новым функциям xi и x2, называемым нормальными координатами. Смысл перехода состоит в получении двух независимых уравнений движения, которые можно решать по отдельности.

Однако, в общем случае эти координаты найти не просто. Поэтому для иллюс­трации такого перехода рассмотрим систему с одинаковыми массами (mi = m2 = m) и

пружинами (ki = k2 = k). Поскольку парциальные частоты совпадают (Wi = Ю2 = Ю =

k + k' k'

), а также ai = a2 = a =---------------------------------- , то система уравнений (3.2i) становится более

m m

простой. Сложив оба уравнения, получаем:

x i =—(ю2 + a)xi, (3.22а)

где xi = si + s2 — первая нормальная координата. Вычитая второе уравнение из перво­го, находим:

x 2 =—(ю2 — a)x 2, (3.22б)

где x2 = si — s2 — вторая нормальная координата. Теперь уравнения (3.22) независимы. Первое из них описывает колебание центра масс системы с частотой

2 2 k'

w2 =w2---------- , (3.23)

m

меньшей парциальной частоты Ю. Второе уравнение описывает изменение расстояния между двумя массами с частотой

2 2 k

w2i = w2 + — , (3.24)

m

превышающей парциальную частоту. Решения уравнений (3.22) очевидны:

xi(t) = si(t) + s2(t) = xoi sin(wit + ji); (3.25а)

x2 (t) = si (t) — s2 (t) = x02 sin(wIIt + jlI). (3.25б)

Возвращаясь к функциям si и s2 , получаем:

x x

si (t) = —0isin(Wi t + ji) +—02sin(Wiit + j ii ); (3.26а)

x x

s2(t) = -~йп(ю1t + j i) ;;2sin(wiit + jn). (3.26б)

Четыре величины Х01, Х02, ФІ и j II определяются из начальных условий: s1 (t = 0), s2(t = 0), .&1 (t = 0), s2(t = 0).

Проиллюстрировав переход к нормальным координатам, вернемся к методике анализа колебаний в произвольных системах, описываемых уравнениями (3.21).

02

Пусть в системе происходит нормальное колебание с неизвестной пока часто­

той ю и коэффициентом распределения амплитуд V =

01

s1(t) = s01 sin^t + ф), s2(t) = s02 sin^t + ф). (3.27)

Подставим (3.27) в систему уравнений (3.21). Тогда получим систему из двух алгебраических уравнений:

(ю12 - ю2>01 + a1s02 = 0;

а 2 s01 + (ю2 — ю2 )s02 = 0.

(3.28)

Система линейных однородных уравнений (3.28) имеет отличные от нуля реше-

ния только в том случае, если ее определитель равен нулю:

22 О»! — ю а 2

а1 22 ю2 —ю

= (ю? — ю2)(ю2 — ю2) — а1 а 2 = 0.

(3.29)

Это — квадратное уравнение относительно ю, причем ю > 0 . Поэтому, решая уравнение (3.29), можно найти нормальные частоты юІ и юІІ. После нахождения частот не составляет труда найти конфигурацию мод, т. е. коэффициенты распределения ампли­туд VІ и VII. Их можно определить, например, из первого уравнения (3.28), причем оче­видно, что для каждой нормальной частоты (юІ или юІІ) эти коэффициенты различны:

22 ю[ — а>! а1

юи — ю12 а1

02

02

(3.30)

VI =

V її =

01

01

Таким образом, уравнение (3.29) и равенство (3.30) позволяют полностью рас­считать параметры каждой из двух мод. Движение каждой из масс, как уже неоднократ­но отмечалось, является суперпозицией двух нормальных колебаний: s1 (t) = s01I Йп(ю^ + ФI) + s01II Йп(юї^ + Фїї), s2 (t) = VI • s01I sin(юIt + Фї) + VII • s01II sin(юIIt + Фїї), где амплитуды s01i и s01ii и начальные фазы ф I и фІІ определяются, как и раньше, из начальных условий: s1 (0) , s2 (0) , s&1 (0) , s&2 (0) .

Расчет мод для любой системы двух связанных осцилляторов читатель может проделать самостоятельно.

Соотношение между парциальными и нормальными частотами. Для уста­новления связи между парциальными и нормальными частотами перепишем (3.29) в виде

(ю^ —ю2)(ю2 —ю2) — у2ю2ю2 = 0, (3.31)

где

2

а1а

12

22

юг ю2 (k1 + k )(k2 + k )

| ^ Безразмерный коэффициент связи g

0 wI wj w2 w II w между двумя системами может принимать значе-

Рис. 5. р. ния 0 < g < i. Если из (3.3i) определить нормаль­

ные частоты WI и WII, то они будут выражаться через парциальные частоты Wi и Ю2 и коэффициент g. Эти четыре частоты будут располагаться на оси частот в последователь­ности, изображенной на рис. 3.9.

При слабой связи (g << i) нормальные частоты близки к парциальным, а при сильной связи (g < i) различие в частотах становится существенным. Это хорошо вид­но, если парциальные частоты совпадают (Wi = W2 = W0). Тогда (3.3i) примет вид:

(Ю2 — Ю2)2 — g 2w4 = 0.

Отсюда

W2 =w0 (i — g), Юц =w2 (i + g). (3.33)

Затухание колебаний. Если энергия не подводится извне, то колебания связан­ных осцилляторов будут затухать. Поскольку сила вязкого трения пропорциональна ско­рости, то уравнения (3.2i) с учетом затухания примут вид:

si = —w2 si — 25is i — ais2,

2 „в ■ (3.34)

s 2 = a 2 si W2 s2 252s 2.

Здесь 5i = ri / 2mi и 52 = Г2 / 2m2 — коэффициенты затухания для первого и второго осцилляторов. Если искать решение этой системы в виде нормальных затухаю­щих колебаний:

si(t) = s0ie—5t sin(wt + j), s2(t) = s02e—5t sin(wt + j), (3.35)

то после подстановки (3.35) в (3.34) можно найти нормальную частоту w, коэффициент затухания 5 и конфигурацию V каждой из двух мод. Опуская промежуточные выклад­ки, отметим, что при wi >> 5i и w2 >> 52 (слабое затухание) нормальные частоты и распределение амплитуд в модах будут близки к тем, что и в отсутствие затухания. Для коэффициента затухания 5 получается выражение:

я_ (ю? — w2)Si + (ю2 — ю2)52

5 /2 2 / 2 2 . (3.36)

(ю? — ю2) + (ю2 — ю2) v ’

Можно видеть, что при произвольном соотношении между Wi, Ю2 , Si и S2 коэффициенты затухания мод SI и SII, получаемые из (3.36) при W = WI и W=WII, будут различными.

Если парциальные частоты совпадают (wi = Ю2), то

S і =S ii = ^(51 +S ii) . (3.37)

Если wi Ф ю2 , а 5i = 52 =5, то

51 =5II =5 . (3.38)

Последним результатом мы воспользуемся при рассмотрении диссипации энер­гии в связанной колебательной системе.

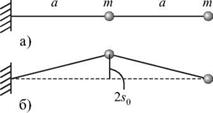
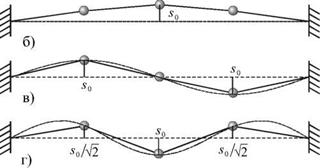
Энергия колебательной системы и ее диссипация. Рассмотрим колебания двух одинаковых масс (рис. 3Л0а), закрепленных на растянутом легком резиновом шнуре.

Если один из грузов оттянуть на расстояние 2s0 (б) и затем одновременно от­пустить обе массы, то их ко­лебания будут иметь вид би­ений. С другой стороны, при этих начальных условиях бу­дут возбуждены две моды (в и г) с одинаковыми амплиту­дами колебаний обеих масс, равными s0 . Энергия, запа­сенная в первой моде, равна сумме кинетических энергий обеих масс при прохождении ими положения равновесия со скоростью = s0 wI, т. е.:

E0 = 2-2(v0і)2 = ms 2 ю2:

(3.39а)

а энергия второй моды, аналогично, равна

E01 = 2 m-(v 01)2 = ms 2 ю2і. (3.39б)

Важно отметить, что энергообмен между модами отсутствует, а полная энергия системы равна сумме энергий ее мод. В то же время в процессе биений энергия первого осциллятора за время, равное половине периода биений, «перетекает» ко второму ос­циллятору и затем за такое же время возвращается обратно. Полный энергообмен меж­ду осцилляторами возможен лишь тогда, когда обе массы одинаковы и отношение (ю1 + wII)/(wII — ю1) равно целому числу n, т. е.:

w і + w її 2w0

= n.

Wii — Wi W б (3.40)

Следовательно, частота w0 должна быть кратной частоте биений. В самом деле, при выполнении условия (3.40) каждая из масс будет периодически останавливаться в положении равновесия (как следует из формул (3.17)). С течением времени колебания будут затухать, и будет экспоненциально уменьшаться энергия, запасенная в модах:

E I(t) = ms0 e —25t ю2 = E0 e—25t, (3.41а)

E II(t) = ms^e—25t Юц = El^e—25t. (3.41б)

Важно подчеркнуть, что через время t E = — энергия каждой из мод умень-

25

шится в е раз, при этом противофазная мода «потеряет» больше энергии, чем синфазная, поскольку начальная энергия E01 у нее была больше, чем E0 (см. (3.39)).

Вынужденные колебания. Рассмотрим основные закономерности вынужден­ных установившихся колебаний в системе, изображенной на рис. 3.11, если на левую массу m1 действует сила F(t) = F0 sin wt. Уравнения движения в этом случае будут отли­чаться от (3.34) наличием этой силы в правой части первого уравнения:

si = —Wj si — 25isi — ais2 +—sin wt,

(3.42)

F(t) k'

m

s'2 = —a 2 si — w? s? — 25 2 s j. Нетрудно догадаться, что k 1 mi

решениями этой системы в уста­новившемся режиме являются гармонические функции Рис 3

si(t) = s0i sin(wt + ji), s2(t) = s02 sin(wt + j2), (3.43)

которые отражают тот факт, что обе массы колеблются на частоте вынуждающей силы. Подставляя (3.43) в (3.42), можно вычислить амплитуды и фазы вынужденных колеба­ний. Мы ограничимся лишь обсуждением результатов.

Рис. 3.12.

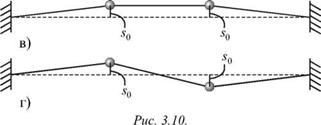
На рис. 3.12 изображена АЧХ для первого осциллятора, к которому приложена сила. Обращает на себя внимание наличие двух резонансов, которые при малом затуха­нии наблюдаются на нормальных частотах wI и wII. При изменении частоты w от wI до WII амплитуда s0i падает и достигает ми­нимума на второй парциальной частоте Ю2 , при этом с уменьшением затухания амплиту­да на этой частоте стремится к нулю. Это обстоятельство используют для подавления отклика системы на действие внешней силы. В радиотехнике, где используются связан­ные колебательные контуры, их применяют как фильтры и демпферы.

Два резонанса имеют место и для смещения s2 второй массы. Если проанализи­ровать отношение амплитуд s02 /s0i в зависимости от частоты w, то оказывается, что это отношение вблизи частоты wI равно коэффициенту распределения амплитуд VI для первой моды, а вблизи частоты wII — коэффициенту распределения амплитуд VII для второй моды. Это используется для определения этих коэффициентов, поскольку при вынужденных колебаниях это сделать проще, чем при собственных.

Колебания систем со многими степенями свободы. Основные идеи, сформулиро­ванные при рассмотрении колебаний систем с двумя степенями свободы, теперь могут быть с успехом использованы для анализа колебаний систем с тремя, четырьмя, ..., N степенями сво­боды, и в пределе, при N ® ¥, для анализа колебаний в сплошных средах, т. е. волн.

Обратимся вначале к колебаниям трех одинаковых масс m, закрепленных на рав­ных расстояниях а на натянутом легком резиновом шнуре, как показано на рис. 3Л3а. Лю­бое колебание этой системы может быть представлено как суперпозиция трех нормальных колебаний с частотами wI, WII и wIII. Опуская на время вопрос о величине частот, найдем конфигурацию этих мод. Примем во внимание, что квадрат частоты колебаний каждой мас­сы в данной моде должен быть одинаков. Этого можно добиться в случае, когда отношения

m О-

m О-

m О-

возвращающей силы к величине массы m и ее смещению s у всех гру­зов будут одинаковыми. Такие условия реали­зуются при смещении масс тремя способами (б, в и г на рис. 3.13). При отпускании грузов из положения (б) в сис­теме будет происходить первое нормальное ко­лебание на частоте wr; из положения (в) — второе на частоте wn ; из положения (г) — третье на частоте Юш. Очевидно, что Юш > wn > WI. Конфигурация каждой из мод может быть описана с помощью двух коэффици­ентов распределения амплитуд. Забегая вперед, отметим, что для четырех масс таких коэффициентов должно быть три, и т. д. Однако ситуация может быть упрощена, если обратить внимание, что расположе­ние масс в позициях (б), (в) и (г) на рис. 3.13 напоминает «синусоидальное» (пунктиром изображен фрагмент функции sin kx, где k — некоторый параметр, характеризующий пе­риод этой функции). Тогда конфигурация первой моды будет описана следующим образом:

а)

Рис. 3.13.

w,

w,,

p 4a

s0(x) = s0 sin kI x; s0[(x) = s0 sin kцx;

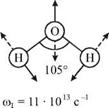
(3.44а) (3.44б) (3.44в) Роль безразмерных коэффициентов V выполняет функция sinkpx (p = I, II, III), вычис­ленная в точках x = x1 = a, x = x2 = 2a, x = x3 = 3a. Другими примерами связанных осцилляторов являются атомы в молекулах CO2, H2O и т. д. На рис. 3.14 изображены конфигурации мод и приведены значения частот нормальных колебаний молекул. Обратим внимание, что эти частоты имеют порядок величины (1013 ^1014) с-1 и значительно превышают (на несколько порядков) частоты механических колебаний макроскопических систем. Резонансные колебания этих (и дру­гих) молекул можно возбудить при взаимодействии разноименно заряженных ионов, составляющих эти молекулы, с электрическим полем световой электромагнитной волны инфракрасного (ИК) диапазона, имеющей близкую частоту.

Для второй моды: Для третьей моды:

= 2k j.

S011 (x) = So sin kшx; kш = 3kj.

юш = 4,78 • 10 13 c 1

Гоц = 11,27 • 10 1 3 c -1 Рис. 3.14.

O H H H

В курсе «Оптика» мы познакомимся с таким взаимодействием, приводящим, в частности, к ослаблению (поглощению) энергии световой волны и ее рассеянию в среде с колеблющимися молекулами (комбинационному рассеянию).

Будем увеличивать число масс, закрепленных на шнуре через равные промежутки а. Если N— число этих масс, то полная длина шнура равна 1 = a (N +1) (рис. 3.15). Рассчитаем нормальные частоты всех мод и их конфигурации. Будем считать, что невесомый шнур натя­нут с силой F, и при малых отклонениях масс от положения равновесия s << 1 эта сила не меняется. Каждая масса испытывает действие сил натяжения шнура по обе стороны от нее.

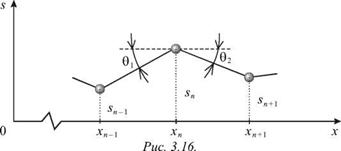
На рис. 3.16 показано мгновенное положение фрагмента шнура и трех масс. Если углы 01 и 82 малы, то возвращающая сила, действующая на среднюю массу, равна:

f = - F • (sin 01 + sin 02) » - F(0j + 02). (3.45)

Величины углов 01 и 02 определяются взаимным расположением масс:

aa С учетом (3.45) и (3.46) уравнение движения средней массы примет вид: Z7( Sn Sn-1 Sn Sn+1 ms n = - F —-------------- —---- + —---- — a a v Если колебания являются нормальными, то

sn - sn+1

Sn-1 (t )= S0,n-1 sin sn (t)= s0,n sin wt, Sn+1 (t )= S0,n+1 sin wt,

n—1 .

0,

02

(3.46) (3.47) (3.48)

где частоту w и распределение амплитуд предстоит определить.

a m a m a m a m a m a m a m a m

J О------------------ О О—о—о—о--- о

(3.49)

2 -

= 0.

30,n+1

0,n

Подставляя (3.48) в (3.47), получим / ,2 ^

0,и-1 '

maw

, N, то (3.49) представляет собой систему N линейных

Поскольку n = 1, 2, 3 однородных уравнений.

Из условия равенства нулю ее определителя можно рассчитать все N нормальных частот, а за­тем для каждой из этих частот определить рас­пределение амплитуд в каждой моде, число которых, очевидно, будет равно N.

Мы же используем уже описанный ранее более легкий путь и будем искать кон­фигурацию каждой моды в виде «синусоидальной» конфигурации:

s0(x) = s0 sin kx, или s0n = s0(xn), (3.50)

где x1 = a, x2 = 2a,...,xn = na,..., xN = Na.

Убедимся, что конфигурация (3.50) удовлетворяет уравнению (3.49), которое перепишем в виде:

(3.51)

s0,n+1 + s0,n-1 2W2 - w2

0,n

где W2 =

Подставим (3.50) в левую часть (3.51): sin k(n + 1)a + sin k(n - 1)a

2W2 - w2

= 2cos ka =

(3.52)

sin kna W 2

Очевидно, что (3.50) удовлетворит уравнению (3.49), если подобрать для данно­го k подходящую частоту w.

Параметр k назовем волновым числом. Объяснение этому будет дано в после­дующих лекциях. Этот параметр должен быть таким, чтобы на концах закрепленного шнура удовлетворялись граничные условия. При x = 0 эти условия выполняются: sin(k • 0) = 0 . На другом конце, где x = a(N +1), потребуем, чтобы

sin ka( N +1) = 0, (3.53)

откуда получаем:

pp

(3.54)

kpa(N +1) = p • p, или k = -

pv ' ^ p a(N +1)!

где целое число p = I, II, ..., N характеризует номер моды (количество мод, как было

показано выше, равно N). Каждой _р-ой моде соответствует своя частота, которая легко

находится из уравнения (3.52):

pp N +1

1 - cos

(3.55)

w2 = 2W2(1 - cos kpa) = 2W2

Рис. 3.17.

Зная волновые числа kp и нормальные частоты wp, не составляет труда записать выражения для смещений всех масс, как функций времени. Для р-ой моды можно записать:

(x„,О = s0p sinkPx„ • sin(wpt + фр); (3.56)

здесь xn = na; n =1, 2, ..., N.

Амплитуда s0p и начальная фаза фp определяются начальными условиями, а k р и wр — свойствами самой системы (формулы (3.54) и (3.55)).

В силу линейности колебательной системы в самом общем случае колебаний получаем для смещения всех частиц выражение:

s(xn, О = Х (x«, г)’ (3.57)

p

где суммирование проводится только по тем модам, которые «участвуют» в колебаниях.

Так, например, удерживая все время среднюю массу в положении равновесия, мы не можем возбудить моды с нечетными номерами p = I, III, ..., поскольку эти моды «требуют» смещения центральной массы.

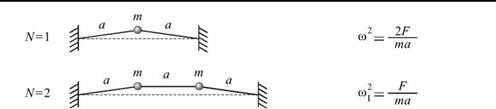
Пользуясь формулой (3.55), нетрудно вычислить нормальные частоты колеблю­щихся масс на шнуре.

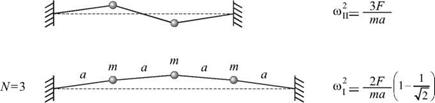
На рис. 3.17 изображены моды колебаний в системе с одной, двумя и тремя массами и для каждой моды указаны величины нормальных частот.

В заключение отметим, что связь типа (3.55) между частотой w и волновым числом k называется дисперсионным соотношением. Это соотношение будет далее ис­пользовано при анализе распространения волн в периодических структурах.